
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Период затухающих колебаний Т определится по формуле
 . (23.8)
. (23.8)
При малом затухании период затухающих колебаний можно приближенно считать равным периоду незатухающих
 (формула Томсона). (23.9)
(формула Томсона). (23.9)
Напряжение на конденсаторе UC, сила тока в контуре I, напряжение на катушке индуктивности UL, так же как и заряд, совершают затухающие колебания, поскольку они связаны с зарядом,
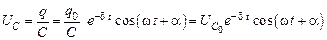 ,
,
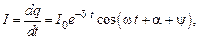
где 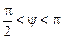 .
.
Для количественной характеристики затухания вводят логарифмический декремент
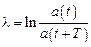 . (23.10)
. (23.10)
Под 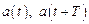 (см. рис. 23.2) понимают соседние амплитуды либо заряда, либо тока, либо напряжения в моменты времени t и (t + T). Из (23.10) можно вывести выражение, связывающее
(см. рис. 23.2) понимают соседние амплитуды либо заряда, либо тока, либо напряжения в моменты времени t и (t + T). Из (23.10) можно вывести выражение, связывающее 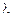 ,
,  и Т,
и Т,

Заменив в последнем выражении d и Т формулами (23.3) и (23.8),
получим
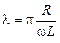 . (23.11)
. (23.11)
При малом затухании
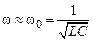
и
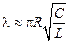 . (23.12)
. (23.12)
|
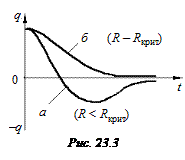 С увеличением сопротивления контура коэффициент затухания растет, частота w уменьшается (23.7), а период затухающих колебаний увеличивается. При некотором сопротивлении контура период становится равным бесконечности, а частота колебаний обращается в нуль (Т = ¥, w = 0). В этом случае в контуре вместо колебаний происходит апериодический разряд конденсатора (рис. 23.3, кривая б).
С увеличением сопротивления контура коэффициент затухания растет, частота w уменьшается (23.7), а период затухающих колебаний увеличивается. При некотором сопротивлении контура период становится равным бесконечности, а частота колебаний обращается в нуль (Т = ¥, w = 0). В этом случае в контуре вместо колебаний происходит апериодический разряд конденсатора (рис. 23.3, кривая б).
Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим Rкрит.. Величину критического сопротивления определяют из условия 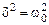
 . (23.13)
. (23.13)
Для определения качества контура как колебательной системы часто используется, в частности в радиотехнике, особый параметр – добротность контура Q. Выясним физический смысл этого параметра.
Рассмотрим собственные колебания в контуре, которые описывает уравнение (23.6). Энергия, запасенная в контуре в начальный момент времени 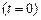 , пропорциональна квадрату амплитуды колебаний
, пропорциональна квадрату амплитуды колебаний
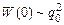 .
.
Через один период (t = Т) эта энергия будет равна
 .
.
Изменение энергии колебаний за период Т, отнесенное к начальной энергии, равно
 .
.
Относительное изменение энергии за время, в течение которого фаза колебаний возрастает на 1 радиан, равно
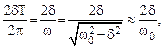
где последнее выражение верно при d << w0 (малое затухание).
Обратная величина
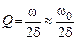
называется добротностью колебательного контура (последнее выражение верно при d << w0).
Приведем другие выражения для измерения добротности [1, 2]
 (23.14)
(23.14)
где l – логарифмический декремент колебаний, R – активное сопротивление контура.
Дата добавления: 2014-10-31; просмотров: 400; Мы поможем в написании вашей работы!; Нарушение авторских прав |