Методические указания. Компьютерная обработка И.В

Компьютерная обработка И.В. Чурина

Тем план 2012 г, поз.

В печать 15.03.2012.

Формат 60x84/16. Бумага тип №3. Офсет.

Объем 3,25 усл.п.л. Заказ № 148 Тираж 500 экз. Цена свободная

________________________________________________________

Издательский центр ДГТУ

Адрес университета и полиграфического предприятия:

344000, г. Ростов-на-Дону, пл. гагарина, 1.

КОЛЕБАНИЯ И ВОЛНЫ

Методические указания

к лабораторным работам по физике № 21, 23, 25–27

для студентов I – II курсов всех факультетов

НОВОСИБИРСК

УДК 534 (076.5)

К 602

Составители:

д-р техн. наук Г. Е. Невская (лаб. работа № 27),

канд. техн. наук А. М. Погорельский (лаб. работа № 25 – 27),

канд. физ.-мат. наук Н. Я. Усольцева (лаб. работа № 23),

канд. техн. наук В. В. Христофоров (лаб. работа № 21, 25),

канд. техн. наук А. В. Морозов (лаб. работа № 21, 25),

асп. А. А. Шевченко (лаб. работа № 21, 25)

Рецензент канд. физ.-мат. наук А. В. Баранов

Работа подготовлена на кафедре общей физики

ÓНовосибирский государственный

ОГЛАВЛЕНИЕ

Лабораторная работа № 21. ИЗУЧЕНИЕ СЛОЖЕНИЯ

КОЛЕБАНИЙ.................................................................................................... 4

Лабораторная работа № 23. СВОБОДНЫЕ ЭЛЕКТРО-

МАГНИТНЫЕ КОЛЕБАНИЯ.................................................................... 14

Лабораторная работа № 25. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ

КОНТУРЕ ....................................................................................................... 23

Лабораторная работа № 26. СТОЯЧИЕ ВОЛНЫ НА СТРУНЕ......................... 37

Лабораторная работа № 27. ИЗУЧЕНИЕ СЛОЖЕНИЯ

СИНХРОННЫХ ОДНОНАПРАВЛЕННЫХ

КОЛЕБАНИЙ................................................................................................. 46

Лабораторная работа № 21

ИЗУЧЕНИЕ СЛОЖЕНИЯ КОЛЕБАНИЙ

Цель работы –с помощью осциллографа изучить сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

Методические указания

Работа включает следующие этапы.

1. Для изучения сложения двух одинаково направленных гармонических колебаний с равными частотами собирают схему, показанную на рис. 21.1. Схема состоит из звукового генератора ЗГ, подключенного к цепочке последовательно соединенных активного сопротив-

ления R и реактивного (емкостного или индуктивного) сопротивле-
ния Х. Вход канала I осциллографа (ОСЦ) подключен к точкам 1 и 3 и, следовательно, на него подается сигнал непосредственно с ЗГ. Вход канала II подключен к точкам 2 и 3, на него подается напряжение с реактивного сопротивления Х. Каналы ОСЦ включаются таким образом, чтобы оба поступающих на них сигнала отклоняли луч на экране ОСЦ вдоль вертикальной оси y. Генератор развертки осциллографа должен быть включен. Это позволяет наблюдать изменение сигналов со временем.

Колебания напряжения на сопротивлении Х являются вынужденными и происходят с частотой колебаний сигнала ЗГ. Следовательно, на каналы I и II осциллографа подаются гармонические колебания
с равными частотами.

Известно [2, 3], что между вынужденными колебаниями напряжения на реактивном сопротивлении Х в последовательной RХ-цепочке и колебаниями генератора ЗГ имеется сдвиг по фазе, величина которого зависит от частоты вынужденных колебаний n, а также от значений сопротивлений R и Х.

Рис. 21.1

Теоретически сложение однонаправленных гармонических колебаний удобно осуществлять с помощью метода векторных диаграмм [1].

Пусть напряжения, поступающие на первый и второй каналы ОСЦ
с ЗГ и реактивного сопротивления соответственно, изменяются по закону

, (21.1)

, (21.2)

где w – циклическая частота колебаний.

Пользуясь методом векторных диаграмм, можно показать, что суммарное напряжение будет определяться выражением

, (21.3)

где

, (21.4)

(21.5)

Из формулы (21.4) видно, что только при отсутствии сдвига фаз амплитуда суммарных колебаний равна сумме амплитуд складываемых колебаний . Если же 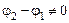, то .

В экспериментах сдвиг фаз между двумя колебаниями с одинаковыми частотами удобно определять путем их сравнения с использованием двухканального режима работы осциллографа. При этом один из сигналов подается на вход первого канала, а другой – на вход второго. Генератор развертки должен быть включен.

Рис. 21.2

По осциллограмме (рис. 21.2) сдвиг фаз между колебаниями вычисляют по формуле

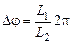(в градусах) или (в радианах).

В данной лабораторной работе сложение колебаний, одно из которых подаётся на первый, а другое – на второй канал, осуществляется автоматически самим осциллографом при включении нужных управляющих кнопок.

Важно отметить, что колебания напряжения на ЗГ представляют собой сумму колебаний напряжения на последовательно соединенных активном R и реактивном X сопротивлениях. Зная характеристики колебаний на ЗГ и X, можно определить характеристики колебаний на R.

2. Для изучения сложения двух взаимно перпендикулярных гармонических колебаний с одинаковыми частотами также используют схему рис. 21.1. С помощью управляющих кнопок осциллографа ОСЦ отключают генератор развертки и отклонение луча одного из каналов с оси y меняют на отклонение вдоль оси x. При этом траектория луча на экране осциллографа будет результатом сложения тех же колебаний (21.1) и (21.2), но как взаимно перпендикулярных.

Исключив из формул (21.1) и (21.2) время, можно получить уравнение этой траектории [1]

(21.6)

где – разность фаз складываемых колебаний. Это уравнение эллипса, ориентация которого относительно осей x и y и форма определяются величиной разности фаз Dj и амплитудами колебаний. Из уравнения (21.6) следует, что, получив в опыте при сложении взаимно перпендикулярных колебаний на экране осциллографа эллипс и измерив в делениях шкалы экрана показанные на рис. 21.3 параметры, можно определить амплитуды и разность фаз складываемых колебаний по формулам

;

;

.

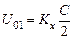Здесь K_x, K_y – коэффициенты усиления осциллографа по осям x и y соответственно, измеряемые в В/дел.

3. Если частоты складываемых взаимно перпендикулярных колебаний n_х и n_у не равны друг другу, то траектория уже не будет эллипсом. В общем случае она имеет вид сложной незамкнутой линии. Только когда частоты колебаний n_х и n_у относятся как целые числа, получают замкнутые траектории, называемые фигурами Лиссажу.

Рис. 21.3

x y Рис. 21.4

Форма фигуры Лиссажу позволяет определить отношение частот складываемых колебаний. Для этого достаточно подсчитать число пересечений фигуры с осью x и осью y. Если ось координат проходит через точку пересечения ветвей фигуры Лиссажу, то эту точку считают дважды.

Для фигуры Лиссажу, изображенной на рис. 21.4, число пересечений ее ветвей с осью x равно n_х = 2, а с осью y – n_у = 4. Можно показать, что отношение частот складываемых колебаний связано с числом пересечений формулой

. (21.7)

Для примера, представленного на рис. 21.4, это отношение: .

Эллипс – простейшая фигура Лиссажу, для которой .

Пользуясь методом фигур Лиссажу, удобно сравнивать частоты складываемых колебаний. Например, можно с помощью эталонного генератора градуировать шкалу генератора неизвестных частот.

Для получения фигур Лиссажу собирают схему рис. 21.5. Схема состоит из генератора переменного напряжения ГПН, звукового генератора ЗГ и осциллографа ОСЦ. Сигналы с ГПН и ЗГ подаются на каналы I и II осциллографа, включенные как отклоняющие луч во взаимно перпендикулярных направлениях.

4. Изучение сложения двух одинаково направленных колебаний с различными частотами и возможно также с помощью схемы рис. 21.5. При этом каналы I и II осциллографа включают так, чтобы оба поступающих на них сигнала отклоняли луч вдоль вертикальной оси у. Включают также генератор развертки осциллографа и режим сложения сигналов.

Рис. 21.5

Расчет показывает [1], что при одинаковых амплитудах складываемых колебаний напряжения ( 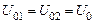) и при нулевых начальных фазах ( ) сигналов

и

суммарное колебание будет определяться выражением

. (21.8)

Полученное суммарное колебания не является гармоническим.

Если Dw = w₁ – w₂ << w_1,2 , т. е. частоты складываемых колебаний мало отличаются друг от друга, то колебания (21.8) называют биениями (рис. 21.6). Биения приближенно можно рассматривать как гармоничес-

Рис. 21.6

кие колебания с циклической частотой , амплитуда которых медленно меняется по закону

. (21.9)

Частота

(21.10)

называется частотой биений.