Пусть ЭДС источника изменяется по гармоническому закону

. (25.1)

Для замкнутого контура в каждый момент времени справедливо второе правило Кирхгофа, согласно которому с учетом выбранных мгновенных направлений тока и полярности ЭДС

, (25.2)

где U_r = JR = R 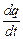— напряжение на общем активном сопротивлении контура; U_C = — напряжение на конденсаторе; e – ЭДС, создающая переменный ток в контуре; e_S = – L – ЭДС самоиндукции в катушке.

Подставляя соответствующие выражения, после преобразований, получаем

. (25.3)

Поскольку при выполнении лабораторной работы, измеряемой величиной будет напряжение на конденсаторе, то перейдем в полученном уравнении к переменной U_C

;

.

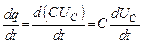Кроме того, введем обозначения:

.

В результате уравнение (25.3) приобретает вид

, (25.4)

где w₀ – циклическая частота собственных незатухающих колебаний в контуре; d — коэффициент затухания.

Общее решение уравнения (25.4) складывается из общего решения соответствующего однородного уравнения U₁ и любого частного решения U₂ неоднородного уравнения (25.4)

.

Известно [1], что если d < w₀ , U₁ равно

, (25.5)

где 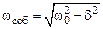— частота собственных затухающих колебаний осциллятора.

Амплитуда этих собственных колебаний зависит от начальных условий и от времени. Со временем она становится пренебрежимо малой и в контуре остаются только вынужденные колеба-
ния U₂ , амплитуда которых от времени не зависит. В этом случае вынужденные колебания называют установившимися. Для них

.

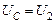Вынужденные колебания становятся с течением времени установившимися и в случае, когда выполняется обратное неравенство:
d > w₀. Разница только в том, что функция уменьшается со временем апериодически.

Частное решение уравнения (25.4) проще всего искать в комплексной форме, заменив в его правой части cos(wt) на e^iwt = cos(wt) + isin(wt). Найдя решение такого уровня в виде комплексной функции , нужно взять действительную часть, т. е. Re , которая и будет искомым решением уравнения (25.4).