Постановка задачи оптимизации при обучении нейронной сети

Пусть имеется нейронная сеть, выполняющая преобразование F:X®Y векторов X из признакового пространства входов X в вектора Y выходного пространства Y. Сеть находится в состоянии W из пространства состояний W. Пусть далее имеется обучающая выборка (Xa,Ya), a = 1..p. Рассмотрим полную ошибку E, делаемую сетью в состоянии W.

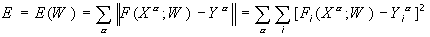
Отметим два свойства полной ошибки. Во-первых, ошибка E=E(W) является функцией состояния W, определенной на пространстве состояний. По определению, она принимает неотрицательные значения. Во-вторых, в некотором обученном состоянии W^*, в котором сеть не делает ошибок на обучающей выборке, данная функция принимает нулевое значение. Следовательно, обученные состояния являются точками минимума введенной функции E(W).

Таким образом, задача обучения нейронной сети является задачей поиска минимума функции ошибки в пространстве состояний, и, следовательно, для ее решения могут применяться стандарные методы теории оптимизации. Эта задача относится к классу многофакторных задач, так, например, для однослойного персептрона с N входами и M выходами речь идет о поиске минимума в NxM-мерном пространстве.

На практике могут использоваться нейронные сети в состояниях с некоторым малым значением ошибки, не являющихся в точности минимумами функции ошибки. Другими словами, в качестве решения принимается некоторое состояние из окрестности обученного состояния W^*. При этом допустимый уровень ошибки определяется особенностями конкретной прикладной задачи, а также приемлимым для пользователя объемом затрат на обучение.

1. Алгоритм обратного распространения ошибки для обучения многослойного персептрона. Недостатки.

Перцептро́н, или персептрон (англ. perceptron от лат. perceptio — восприятие; нем. perzeptron) — математическая и компьютерная модель восприятия информации мозгом (кибернетическая модель мозга), предложенная Фрэнком Розенблаттом в 1957 году и реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером. Несмотря на свою простоту, перцептрон способен обучаться и решать довольно сложные задачи. Основная математическая задача, с которой он справляется, — это линейное разделение любых нелинейных множеств, так называемое обеспечение линейной сепарабельности.

Перцептрон состоит из трёх типов элементов, а именно: поступающие от сенсоров сигналы передаются ассоциативным элементам, а затем реагирующим элементам. Таким образом, перцептроны позволяют создать набор «ассоциаций» между входными стимулами и необходимой реакцией на выходе. В биологическом плане это соответствует преобразованию, например, зрительной информации в физиологический ответ от двигательных нейронов. Согласно современной терминологии, перцептроны могут быть классифицированы как искусственные нейронные сети:

1. с одним скрытым слоем;
2. с пороговой передаточной функцией;
3. с прямым распространением сигнала.

Метод обратного распространения ошибки (англ. backpropagation)— метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. А.И. Галушкиным^[1], а также независимо и одновременно Полом Дж. Вербосом^[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом^[3] и независимо и одновременно С.И. Барцевым и В.А. Охониным (Красноярская группа)^[4].. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.

Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.^[5]

Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.

Архитектура многослойного перцептрона

Алгоритм: BackPropagation

1. Инициализировать маленькими случайными значениями,
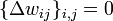
2. Повторить NUMBER_OF_STEPS раз:

Для всех d от 1 до m:

1. Подать на вход сети и подсчитать выходы 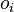каждого узла.
2. Для всех

.

1. Для каждого уровня l, начиная с предпоследнего:

Для каждого узла j уровня l вычислить

.

1. Для каждого ребра сети {i, j}

.

.

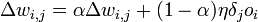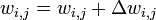1. Выдать значения .

где — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции