Принцип Winner Take All (WTA) - Победитель Забирает Все - в модели Липпмана-Хемминга.

Рассмотрим задачу о принадлежности образа x некоторому классу X_k, определяемому заданными библиотечными образами x_k. Каждый из заданных образов обучающей выборки непосредственно определяет свой собственный класс, и таким образом, задача сводится к поиску "ближайшего" образа. В случае двух двоичных (0-1) образов расстояние между ними может быть определено по Хеммингу, как число несовпадающих компонент. Теперь после вычисления всех попарных расстояний искомый класс определяется по наименьшему из них.

Нейросетевое решение этой задачи может быть получено на основе архитектуры Липпмана-Хемминга (Lippman R., 1987). Сеть имеет один слой одинаковых нейронов, число которых равно количеству классов. Таким образом, каждый нейрон "отвечает" за свой класс. Каждый нейрон связан с каждым из входов, число которых равно размерности рассматриваемых библиотечных образов. Веса связей полагаются равными нормированным библиотечным образам:

Здесь - значение веса связи от n-го входа к m-му нейрону (см. рис.7.1.). Процесс поступления информации о векторе x в нейронную сеть является безитерационным. При этом входной вектор сначала нормируется:

и нейроны принимают начальные уровни активности:

Здесь f(x) - переходная функция (функция активации) нейрона, которая выбирается равной нулю при x<0, и f(x)=x при x>0. Пороги Q полагаются обычно равными нулю.

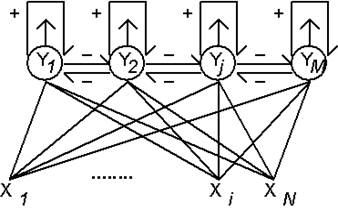
Рис. 7.1. Нейронная сеть Липпмана-Хемминга.

При поступлении входного вектора начальное возбуждение получают все нейроны, скалярное произведение векторов памяти которых с входным вектором превышает порог. В дальнейшем среди них предстоит выбрать один, для которого оно максимально. Это достигается введением дополнительных обратных связей между нейронами, устроенных по принципу "латерального торможения". Каждый нейрон получает тормозящее (отрицательное) воздействие со стороны всех остальных нейронов, пропорционально степени их возбуждения, и испытывает возбуждающее (положительное) воздействие самого на себя. Веса латеральных связей в нейронном слое нормируются таким образом, что суммарный сигнал является возбуждающим только для нейрона с максимальной исходной активностью. Остальные нейроны испытывают торможение:

По выполнении некоторого числа итераций t для всех нейронов кроме одного значение аргумента функции f(x) становится отрицательным, что обращает их активность ym в нуль. Единственный, оставшийся активным, нейрон является победителем. Он и указывает на тот класс, к которому принадлежит введенный образ. Такой механизм получил название "Победитель-Забирает-Все" ( Winner Take All - WTA ). Механизм WTA используется и в других нейросетевых архитектурах. Заложенный в его основе принцип латерального торможения имеет глубокие биологические основания и весьма широко распространен в нейронных сетях живых организмов.

Нейросетевая парадигма Липпмана-Хемминга является моделью с прямой структурой памяти. Информация, содержащаяся в библиотечных образах никак не обобщается, а непосредственно запоминается в синаптических связях. Память здесь не является распределенной, так как при выходе из строя одного нейрона полностью теряется информация обо всем соответствующем ему образе памяти.

1. Сети Кохонена. Структура. Принцип работы.

Сеть Кохонена - это одна из разновидностей нейронных сетей, которые используют неконтролируемое обучение. При таком обучении обучающее множество состоит лишь из значений входных переменных, в процессе обучения нет сравнивания выходов нейронов с эталонными значениями. Можно сказать, что такая сеть учится понимать структуру данных.

Идея сети Кохонена принадлежит финскому ученому Тойво Кохонену (1982 год). Основной принцип работы сетей - введение в правило обучения нейрона информации относительно его расположения.

В основе идеи сети Кохонена лежит аналогия со свойствами человеческого мозга. Кора головного мозга человека представляет собой плоский лист и свернута складками. Таким образом, можно сказать, что она обладает определенными топологическими свойствами (участки, ответственные за близкие части тела, примыкают друг к другу и все изображение человеческого тела отображается на эту двумерную поверхность). Во многих моделях ИНС решающую роль играют связи между нейронами, определяемые весовыми коэффициентами и указывающие место нейрона в сети. Однако в биологических системах, на пример, таких как мозг, соседние нейроны, получая аналогичные входные сигналы, реагируют на них сходным образом, т. е. группируются, образуя некоторые области. Поскольку при обработке многомерного входного образа осуществляется его проецирование на область меньшей размерности с сохранением его топологии, часто подобные сети называют картами (self-organizing feature map). В таких сетях существенным является учет взаимного расположения нейронов одного слоя.

Сеть Кохонена (самоорганизующаяся карта) относится к самоорганизующимся сетям, которые при поступлении входных сигналов, в отличие от сетей, использующих обучение с учителем, не получают информацию о желаемом выходном сигнале. В связи с этим невозможно сформировать критерий настройки, основанный на рассогласовании реальных и требуемых выходных сигналов ИНС, поэтому весовые параметры сети корректируют, исходя из других соображений. Все предъявляемые входные сигналы из заданного обучающего множества самоорганизующаяся сеть в процессе обучения разделяет на классы, строя так называемые топологические карты.

2.1 Структура сети Кохонена

Сеть Кохонена использует следующую модель (рисунок 2.1): сеть состоит из М нейронов, образующих прямоугольную решетку на плоскости — слой.

Рисунок 2.1 – Модель сети Кохонена

К нейронам, расположенным в одном слое, представляющем собой двумерную плоскость, подходят нервные волокна, по которым поступает N-мерный входной сигнал. Каждый нейрон характеризуется своим положением в слое и весовым коэффициентом. Положение нейронов, в свою очередь, характеризуется некоторой метрикой и определяется топологией слоя, при которой соседние нейроны во время обучения влияют друг на друга сильнее, чем расположенные дальше. Каждый нейрон образует взвешенную сумму входных сигналов с , если синапсы ускоряющие, и - если тормозящие. Наличие связей между нейронами приводит к тому, что при возбуждении одного из них можно вычислить возбуждение остальных нейронов в слое, причем это возбуждение с увеличением расстояния от возбужденного нейрона уменьшается. Поэтому центр возникающей реакции слоя на полученное раздражение соответствует местоположению возбужденного нейрона. Изменение входного обучающего сигнала приводит к максимальному возбуждению другого нейрона и соответственно — к другой реакции слоя. Сеть Кохонена может рассматриваться как дальнейшее развитие LVQ (Learning Vector Quantization). Отличие их состоит в способах обучения.

2.2 Обучение сети Кохонена

Сеть Кохонена, в отличие от многослойной нейронной сети, очень проста; она представляет собой два слоя: входной и выходной. Элементы карты располагаются в некотором пространстве, как правило, двумерном.

Сеть Кохонена обучается методом последовательных приближений. В процессе обучения таких сетей на входы подаются данные, но сеть при этом подстраивается не под эталонное значение выхода, а под закономерности во входных данных. Начинается обучение с выбранного случайным образом выходного расположения центров.

В процессе последовательной подачи на вход сети обучающих примеров определяется наиболее схожий нейрон (тот, у которого скалярное произведение весов и поданного на вход вектора минимально). Этот нейрон объявляется победителем и является центром при подстройке весов у соседних нейронов. Такое правило обучения предполагает "соревновательное" обучение с учетом расстояния нейронов от "нейрона-победителя".

Обучение при этом заключается не в минимизации ошибки, а в подстройке весов (внутренних параметров нейронной сети) для наибольшего совпадения с входными данными.

Основной итерационный алгоритм Кохонена последовательно проходит ряд эпох, на каждой из которых обрабатывается один пример из обучающей выборки. Входные сигналы последовательно предъявляются сети, при этом желаемые выходные сигналы не определяются. После предъявления достаточного числа входных векторов синаптические веса сети становятся способны определить кластеры. Веса организуются так, что топологически близкие узлы чувствительны к похожим входным сигналам.

В результате работы алгоритма центр кластера устанавливается в определенной позиции, удовлетворительным образом кластеризующей примеры, для которых данный нейрон является "победителем". В результате обучения сети необходимо определить меру соседства нейронов, т.е. окрестность нейрона-победителя, которая представляет собой несколько нейронов, которые окружают нейрон-победитель.

Сначала к окрестности принадлежит большое число нейронов, далее ее размер постепенно уменьшается. Сеть формирует топологическую структуру, в которой похожие примеры образуют группы примеров, близко находящиеся на топологической карте.

Рассмотрим это более подробнее. Кохонен существенно упростил решение задачи, выделяя из всех нейронов слоя лишь один с-й нейрон, для которого взвешенная сумма входных сигналов максимальна:

. (2.1)

Отметим, что весьма полезной операцией предварительной об работки входных векторов является их нормализация:

(2.2)

превращающая векторы входных сигналов в единичные с тем же направлением.

(2.3)

В этом случае вследствие того, что сумма весов каждого нейрона одного слоя для всех нейронов этого слоя одинакова и , условие (2.1) эквивалентно условию:

. (2.4)

Таким образом, будет активирован только тот нейрон, вектор весов которого w наиболее близок к входному вектору х. А так как перед началом обучения неизвестно, какой именно нейрон будет активироваться при предъявлении сети конкретного входного вектора, сеть обучается без учителя, т. е. самообучается. Вводя потенциальную функцию — функцию расстояния («соседства») между i-м и j-м нейронами с местоположениями и соответственно, монотонно убывающую с увеличением расстояния между этими нейронами, Кохонен предложил следующий алгоритм коррекции весов:

, (2.5)

где - изменяющийся во времени коэффициент усиления (обычно выбирают на первой итерации, постепенно уменьшая в процессе обучения до нуля); - монотонно убывающая функция.

, (2.6)

Где и - векторы, определяющие положение нейронов i и j в решетке. При принятой метрике функция с ростом времени стремится к нулю. На практике вместо параметра времени используют параметр расстояния , задающий величину области «соседства» и уменьшающийся с течением времени до нуля. Выбор функции также влияет на величины весов всех нейронов в слое. Очевидно, что для нейрона-победителя :

. (2.7)

На рисунке 2.2 показан пример изменения двумерных весов карты , образующей цепь. При появлении входного образа наиболее сильно изменяется весовой вектор нейрона-победителя 5, менее сильно — веса расположенных рядом с ним нейронов 3, 4, 6, 7. А так как нейроны 1, 2, 8, 9 лежат вне области «соседства», их весовые коэффициенты не изменяются.

Рисунок – 2.2 Изменение весов карты Кохонена

Таким образом, алгоритм обучения сети Кохонена может быть описан так:

1. Инициализация

Весовым коэффициентам всех нейронов присваиваются малые случайные значения и осуществляется их нормализация. Выбирается соответствующая потенциальная функция и назначается начальное значение коэффициента усиления .

2. Выбор обучающего сигнала

Из всего множества векторов обучающих входных сигналов в соответствии с функцией распределения выбирается один вектор , который представляет «сенсорный сигнал», предъявляемый сети.

3. Анализ отклика (выбор нейрона)

По формуле (2.1) определяется активированный нейрон.

4. Процесс обучения

В соответствии с алгоритмом (2.5) изменяются весовые коэффициенты активированного и соседних с ним нейронов до тех пор, пока не будет получено требуемое значение критерия качества обучения или не будет предъявлено заданное число обучающих входных векторов. Окончательное значение весовых коэффициентов совпадает с нормализованными векторами входов.

Поскольку сеть Кохонена осуществляет проецирование N-мерного пространства образов на М-мерную сеть, анализ сходимости алгоритма обучения представляет собой довольно сложную задачу.

Если бы с каждым нейроном слоя ассоциировался один входной вектор, то вес любого нейрона слоя Кохонена мог бы быть обучен с помощью одного вычисления, так как вес нейрона-победителя корректировался бы с (в соответствии с (2.5) для одномерного случая вес сразу бы попадал в центр отрезка [а, b]). Однако обычно обучающее множество включает множество сходных между собой входных векторов, и сеть Кохонена должна быть обучена активировать один и тот же нейрон для каждого из них. Это достигается усреднением входных векторов путем уменьшения величины, а не при предъявлении каждого последующего входного сигнала. Таким образом, веса, ассоциированные с нейроном, усреднятся и примут значение вблизи «центра» входных сигналов, для которых данный нейрон является «победителем».

2.3 Выбор функции «соседства»

На рисунке 2.3 показан слой нейронов с нейроном-победителем, отмеченным черным кружком. Поскольку веса всех затемненных нейронов изменяются по-разному, в зависимости от их удаленности от нейрона-победителя, наиболее простым является выбор в качестве некоторой величины, равной единице при , меньшей единицы для затемненных нейронов, т. е. нейронов, лежащих в непосредственной близости от активированного нейрона, и нулю для остальных, отмеченных светлыми кружками.

Рисунок 2.3 – Слой нейронов Кохонена

На практике же в качестве выбирают функции, использующие евклидову метрику:

, (2.8)

где , — координаты i-гo и j-го нейронов.

К числу наиболее широко используемых потенциальных функций относятся:

а) колоколообразная функция Гаусса

, (2.9)

где - дисперсия отклонения;

Рисунок 2.4 – Колоколообразная функция Гаусса

б) функция «мексиканская шляпа»

, (2.10)

Рисунок 2.5 – Функция «мексиканская шляпа»

в) косинусоидная функция

(2.11)

Рисунок 2.6 – Косинусоидная функция

г) конусообразная функция

(2.12)

Рисунок 2.7 – Конусообразная функция

д) цилиндрическая функция

(2.13)

Рисунок 2.8 – Цилиндрическая функция

2.4 Карта Кохонена

Как правило, сначала строят довольно грубую карту (модель разбиения), постепенно уточняя ее в процессе обучения. Для этого необходимо медленно изменять не только параметр , но и, например, параметр в формуле (2.9). Одним из эффективных способов изменения этих параметров является следующий:

, (2.14)

, (2.15)

где ; ; ; - параметры, определяющие крутизну функции ; - задаваемое число итераций.

На рисунке 2.9 показан процесс построения карты Кохонена, представляющей собой двумерную решетку, образованную путем соединения соседних нейронов, находящихся в узлах решетки. Исходя из начальных условий и используя алгоритм обучения (2.5), сеть по мере увеличения числа обучающих входных образов развивается и приобретает вид решетки. Внизу каждого рисунка поставлено количество образов, на основании которых получена соответствующая сеть.

Рисунок 2.9 – Построение карты Кохонена

Уникальность метода самоорганизующихся карт состоит в преобразовании n-мерного пространства в двухмерное. Применение двухмерных сеток связано с тем, что существует проблема отображения пространственных структур большей размерности. Имея такое представление данных, можно визуально определить наличие или отсутствие взаимосвязи во входных данных.

Нейроны карты Кохонена располагают в виде двухмерной матрицы, раскрашивают эту матрицу в зависимости от анализируемых параметров нейронов.

На рисунке 2.10 приведен пример карты Кохонена.

Рисунок 2.10 – Пример карты Кохонена

На рисунке 2.11 приведена раскраска карты, а точнее, ее i-го признака, в трехмерном представлении. Как мы видим, темно-синие участки на карте соответствуют наименьшим значениям показателя, красные - самым высоким.

Рисунок 2.11 – Раскраска i-го признака в трехмерном пространстве

Теперь, возвращаясь к рисунку 2.10, мы можем сказать, какие объекты имеют наибольшие значения рассматриваемого показателя (группа объектов, обозначенная красным цветом), а какие - наименьшие значения (группа объектов, обозначенная синим цветом).

Таким образом, карты Кохонена можно отображать:

· в двухмерном виде, тогда карта раскрашивается в соответствии с уровнем выхода нейрона;

· в трехмерном виде.

В результате работы алгоритма получаем такие карты:

а) Карта входов нейронов.

Веса нейронов подстраиваются под значения входных переменных и отображают их внутреннюю структуру. Для каждого входа рисуется своя карта, раскрашенная в соответствии со значением конкретного веса нейрона. При анализе данных используют несколько карт входов. На одной из карт выделяют область определенного цвета - это означает, что соответствующие входные примеры имеют приблизительно одинаковое значение соответствующего входа. Цветовое распределение нейронов из этой области анализируется на других картах для определения схожих или отличительных характеристик.

б) Карта выходов нейронов.

На карту выходов нейронов проецируется взаимное расположение исследуемых входных данных. Нейроны с одинаковыми значениями выходов образуют кластеры - замкнутые области на карте, которые включают нейроны с одинаковыми значениями выходов.

в) Специальные карты.

Это карта кластеров, матрица расстояний, матрица плотности попадания и другие карты, которые характеризуют кластеры, полученные в результате обучения сети Кохонена.

Координаты каждой карты определяют положение одного нейрона. Так, координаты [15:30] определяют нейрон, который находится на пересечении 15-го столбца с 30-м рядом в матрице нейронов. Важно понимать, что между всеми рассмотренными картами существует взаимосвязь - все они являются разными раскрасками одних и тех же нейронов. Каждый пример из обучающей выборки имеет одно и то же расположение на всех картах.

Полученную карту можно использовать как средство визуализации при анализе данных. В результате обучения карта Кохонена классифицирует входные примеры на кластеры (группы схожих примеров) и визуально отображает многомерные входные данные на плоскости нейронов.

При реализации сети Кохонена возникают следующие проблемы:

1. Выбор коэффициента обучения

Этот выбор влияет как на скорость обучения, так и на устойчивость получаемого решения. Очевидно, что процесс обучения ускоряется (скорость сходимости алгоритма обучения увеличивается) при выборе близким к единице. Однако в этом случае предъявление сети различных входных векторов, относящихся к одному классу, приведет к изменениям соответствующего вектора весовых коэффициентов. Напротив, при 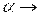0 скорость обучения будет медленной, однако вектор весовых коэффициентов, достигнув центра класса, при подаче на вход сети различных сигналов, относящихся к одному классу, будет оставаться вблизи этого центра. Поэтому одним из путей ускорения процесса обучения при одновременном обеспечении получения устойчивого решения является выбор переменного с 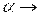1 на начальных этапах обучения и 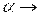0 - на заключительных. К сожалению, такой подход не применим в тех случаях, когда сеть должна непрерывно подстраиваться к предъявляемым ей новым входным сигналам.

2. Рандомизация весов

Рандомизация весов слоя Кохонена может породить серьезные проблемы при обучении, так как в результате этой операции весовые векторы распределяются равномерно по поверхности гиперсферы. Как правило, входные векторы распределены неравномерно и группируются на относительно малой части поверхности гиперсферы. Поэтому большинство весовых векторов окажутся настолько удаленными от любого входного вектора, что не будут активированы и станут бесполезными. Более того, оставшихся активированных нейронов может оказаться слишком мало, чтобы разбить близко расположенные входные векторы на кластеры.

3. Выбор начальных значений векторов весовых коэффициентов и нейронов.

Если начальные значения выбраны неудачно, т. е. расположенными далеко от предъявляемых входных векторов, то нейрон не окажется победителем ни при каких входных сигналах, а, следовательно, не обучится.

На рисунке 2.12 показан случай, когда начальное расположение весов и привело к тому, что после обучения сети все предъявляемые образы классифицируют нейроны с весами , , и . Веса же и не изменились и могут быть удалены из сети.

а б

Рисунок 2.12 – Начальное (а) и конечное (б) положения векторов весов

4. Выбор параметра расстояния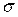

Если сначала параметр 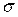выбран малым или очень быстро уменьшается, то далеко расположенные друг от друга нейроны не могут влиять друг на друга. Хотя две части в такой карте настраиваются правильно, общая карта будет иметь топологический дефект (рисунок 2.13).

5. Количество нейронов в слое

Число нейронов в слое Кохонена должно соответствовать числу классов входных сигналов. Это может быть недопустимо в тех задачах, когда число классов заранее известно.

Рисунок 2.13 – Топологический дефект карты

6. Классы входных сигналов

Слой Кохонена может формировать только классы, представляющие собой выпуклые области входного пространства.

2.5 Задачи, решаемые при помощи карт Кохонена

Самоорганизующиеся карты могут использоваться для решения задач моделирования, прогнозирования, кластеризации, поиска закономерностей в больших массивах данных, выявления наборов независимых признаков и сжатии информации.

Наиболее распространенное применение сетей Кохонена - решение задачи классификации без учителя, т.е. кластеризации.

Напомним, что при такой постановке задачи нам дан набор объектов, каждому из которых сопоставлена строка таблицы (вектор значений признаков). Требуется разбить исходное множество на классы, т.е. для каждого объекта найти класс, к которому он принадлежит.

В результате получения новой информации о классах возможна коррекция существующих правил классификации объектов.

Самым распространенным применением карт Кохонена является:

· разведочный анализ данных

· обнаружение новых явлений

В первом случае сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель. Если в данных распознаны классы, то их можно обозначить, после чего сеть сможет решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, - тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами.

Во втором случае сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.

кластеризация нейронный сеть кохонен

1. Сети Хопфилда. Структура. Принцип работы.

Сеть Хопфилда использует три слоя: входной, слой Хопфилда и выходной слой. Каждый слой имеет одинаковое количество нейронов. Входы слоя Хопфилда подсоединены к выходам соответствующих нейронов входного слоя через изменяющиеся веса соединений. Выходы слоя Хопфилда подсоединяются ко входам всех нейронов слоя Хопфилда, за исключением самого себя, а также к соответствующим элементам в выходном слое. В режиме функционирования, сеть направляет данные из входного слоя через фиксированные веса соединений к слою Хопфилда. Структурная схема сети Хопфилда представлена на рис. 1.

Рис. 1. - Схема сети Хопфилда

Сеть Хопфилда состоит из N искусственных нейронов. Граница ёмкости памяти для сети (то есть количество образов, которое она может запомнить) составляет приблизительно 15% от числа нейронов в слое Хопфилда (N*0,15). При этом запоминаемые образы не должны быть сильно коррелированны.

Размерности входныхивыходных сигналов в сети ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации — технологическими возможностями. Размерности входных и выходных сигналов совпадают.

Каждый нейрон системы может принимать одно из двух состояний (что аналогично выходу нейрона с пороговой функцией активации):

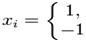
Благодаря своей биполярной природе нейроны сети Хопфилда иногда называют спинами.

Взаимодействие спинов сети описывается выражением («энергетической» функцией, которая уменьшается в процессе функционирования сети):

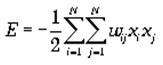
где wijэлемент матрицы взаимодействий W, которая состоит из весовых коэффициентов связей между нейронами. В эту матрицу в процессе обучения записывается М «образов» — N-мерных бинарных векторов: Sm= (sm1,sm2,...,smN).

В сети Хопфилда матрица связей является симметричной (wij= wji), а диагональные элементы матрицы полагаются равными нулю (wii= 0), что исключает эффект воздействия нейрона на самого себя и является необходимым для сети Хопфилда.

Рассмотрим общий алгоритм работы сети:

1. На стадии инициализации сети весовые коэффициенты синапсов (связей, по которым выходные сигналы одних нейронов поступают на входы других) устанавливаются следующим образом:

Где i и j ()– индексы, соответственно, предсинаптического (входного) и постсинаптического (выходного) нейронов; wij— i-й синаптический вес j-го нейрона; xik, xjk– i-ый и j-ый элементы вектора k-ого образца.

1.На входы сети подаётся неизвестный сигнал. Фактически его ввод осуществляется непосредственной установкой значений:

yj(0) = xj , j = 0...n-1,

где yj— аксон (т.е. выход) j-го нейрона. Поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от yjозначает нулевую итерацию в цикле работы сети.

3. Рассчитывается новое состояние нейронов и новые значения аксонов:

,

где j=0...n-1, p – номер (конкретный шаг) итерации, - новое состояние нейрона;

,

где f – активационная функция в виде скачка, приведённая на рис. 2б.

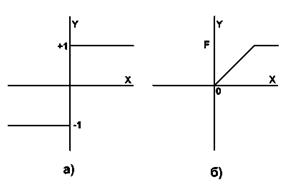
Рис. 2: а) жёсткая пороговая (передаточная)функция сети Хопфилда;

б) активационная функция сети Хопфилда.

4.Проверка: изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.

Алгоритм обучения сети Хопфилда имеет существенные отличия в сравнении с такими классическими алгоритмами обучения перцептронов как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе. Вычисление коэффициентов базируется на следующем правиле: для всех запомненных образов Xiматрица связи должна удовлетворять уравнению:

Поскольку именно при этом условии состояния сети Xiбудут устойчивы - попав в такое состояние, сеть в нём и останется.

Некоторые авторы относят сеть Хопфилда к обучению без учителя. Но это неверно, т.к. обучение без учителя предполагает отсутствие информации о том, к каким классам нужно относить тот или иной образ. Для сети Хопфилда без этой информации нельзя настроить весовые коэффициенты, поэтому здесь можно говорить лишь о том, что такую сеть можно отнести к классу оптимизирующих сетей (фильтров). Отличительной особенностью фильтров является то, что матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются.

В сети Хопфилда есть обратные связи и из-за этого нужно решать проблему устойчивости. Веса между нейронами в сети Хопфилда могут рассматриваться в виде матрицы взаимодействий W. Сеть с обратными связями является устойчивой, если её матрица симметрична и имеет нули на главной диагонали.В случае сети Хопфилда условие симметричности является необходимым, но не достаточным, в том смысле, что на достижение устойчивого состояния влияет ещё и режим работы сети.Ниже будет показано, что только асинхронный режим работы сети гарантирует достижение устойчивого состояния сети, в синхронном случае возможно бесконечное переключение между двумя разными состояниями (такая ситуация называется динамическим аттрактором, в то время как устойчивое состояние принято называть статическим аттрактором).

Расчёт весовых коэффициентов (обучением сети) происходит по следующей формуле :

где N - размерность векторов, m – число запоминаемых выходных векторов; d – номер запоминаемого выходного вектора; Xij– i-я компонента запоминаемого выходного j-го вектора.

Это выражение может стать более ясным, если заметить, что весовая матрица W может быть найдена вычислением внешнего произведения каждого запоминаемого вектора с самим собой и суммированием матриц, полученных таким образом. Это может быть записано в виде

где Xi– i-й запоминаемый вектор-строка.

Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формулам 3-его этапа алгоритма функционирования сети. Полученное устойчивое состояние yj (статический аттрактор), или, возможно, в синхронном случае пара { yj, yj+1} (динамический аттрактор), является ответом сети на данный входной образ.

Существуют 3 режима работы сети Хопфилда:

1) режим фильтрации;

2) синхронный режим;

3) асинхронный режим.

Рассмотрим коротко работу сети в режиме фильтрации (восстановление повреждённых образов). Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формуле нахождения общего алгоритма. Этот процесс называется конвергенцией сети.

Это же можно описать так называемым локальным полем aiдействующим на нейрон xiсо стороны всех остальных нейронов сети:

.

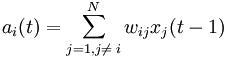После расчёта локального поля нейрона ai(t) это значение используется для расчёта значения выхода через функцию активации, которая в данном случае является пороговой (с нулевым порогом). Соответственно, значение выхода xi(t) нейрона і в текущий момент времени t рассчитывается по формуле:

.

Где xj(t ? 1) - значения выходов нейрона j в предыдущий момент времени.

Обычно ответом является такое устойчивое состояние, которое совпадает с одним из запомненных при обучении векторов, однако при некоторых условиях (в частности, при слишком большом количестве запомненных образов) результатом работы может стать так называемый ложный аттрактор ("химера"), состоящий из нескольких частей разных запомненных образов, а также в синхронном режиме сеть может прийти к динамическому аттрактору. Обе эти ситуации в общем случае являются нежелательными, поскольку не соответствуют ни одному запомненному вектору - а соответственно, не определяют класс, к которому сеть отнесла входной образ.

Рассмотрим коротко работу сети всинхронном режиме работы.Если работа сети моделируется на одном процессоре, то при данном режиме последовательно просматриваются нейроны, однако их состояния запоминаются отдельно и не меняются до тех пор, пока не будут пройдены все нейроны сети. Когда все нейроны просмотрены, их состояния одновременно (т.е. синхронно, отсюда и название) меняются на новые. Таким образом, достигается моделирование параллельной работы последовательным алгоритмом. При реально параллельном моделировании, этот режим фактически означает, что время передачи ?ijдля каждой связи между элементами uiи ujодинаковое для каждой связи, что приводит к параллельной работе всех связей, они одновременно меняют свои состояния, основываясь только на предыдущем моменте времени. Наличие таких синхронных тактов, которые можно легко выделить и приводит к пониманию синхронного режима. При синхронном режиме возможно (хотя и далеко не всегда наблюдается) бесконечное чередование двух состояний с разной энергией (динамический аттрактор). Поэтому синхронный режим практически для сети Хопфилда не используется, и рассматривается лишь как основа для понимания более сложного асинхронного режима.

Рассмотрим коротко работу сети васинхронном режиме работы сети.Если моделировать работу сети как последовательный алгоритм, то в данном режиме работы состояния нейронов в следующий момент времени меняются последовательно: вычисляется локальное поле для первого нейрона в момент t, определяется его реакция, и нейрон устанавливается в новое состояние (которое соответствует его выходу в момент t+1), потом вычисляется локальное поле для второго нейрона с учётом нового состояния первого, меняется состояние второго нейрона, и так далее - состояние каждого следующего нейрона вычисляется с учетом всех изменений состояний рассмотренных ранее нейронов.По сути при последовательной реализации сети Хопфилда явно не видно в чём заключается асинхронность, но это видно если сеть Хопфилда реализовать с параллельными вычислениями. В этом случае асинхронный режим сети Хопфилда упрощён, и носит частный случай по сравнению с общим видом асинхронных сетей, где время передачи ?ijдля каждой связи между элементами uiи ujсвое, но постоянное. Чтобы рассмотреть работу сети при параллельной реализации, необходимо ввести понятие такта - как минимальное время за которое происходит передача сигнала по связи, т.е. при ?ij= 1. Тогда за промежуток времени между t и (t+1) происходит определённое количество тактов N. И именно в пределах времени из N тактов происходит асинхронность протекания сигналов и выполнения расчётов. То есть, например, когда нужно рассчитать состояние нейрона №3 необходимо рассчитать состояния нейрона №1 и состояния нейрона №2 и умножить это на соответствующие веса (рис.1). Но оказывается, для того чтобы рассчитать состояние нейрона №2 нам нужно знать обновленное состояние нейрона №1 и старое состояние нейрона №3, умножить их на соответствующие веса. Понятно, что физически невозможно рассчитать состояние нейрона №1 и состояние нейрона №2 за одно и то же время, т.к. состояние нейрона №2 зависит от состояния нейрона №1. Поэтому связь между нейроном №1 и нейроном №3 имеете время передачи ?ij= 2, и достигает нейрона №3 за два такта. Именное такое разное время передачи ?ijи позволяет говорить о сети Хопфилда как о сети с асинхронным режимом.

В асинхронном режиме невозможен динамический аттрактор - вне зависимости от количества запомненных образов и начального состояния, сеть непременно придет к устойчивому состоянию (статическому аттрактору).

1. Правило обучения Хебба для сети Хопфилда.

Правило обучения для сети Хопфилда опирается на исследования Дональда Хебба (D.Hebb, 1949), который предположил, что синаптическая связь, соединяющая два нейрона будет усиливатьося, если в процессе обучения оба нейрона согласованно испытывают возбуждение либо торможение. Простой алгоритм, реализующий такой механизм обучения, получил название правила Хебба. Рассмотрим его подробно.

Пусть задана обучающая выборка образов x a, a = 1..p. Требуется построить процесс получения матрицы связей W, такой, что соответствующая нейронная сеть будет иметь в качестве стационарных состояний образы обучающей выборки (значения порогов нейронов T обычно полагаются равными нулю).

В случае одного обучающего образа правило Хебба приводит к требуемой матрице:

Покажем, что состояние S=x является стационарным для сети Хопфилда с указанной матрицей. Действительно, для любой пары нейронов i и j энергия их взаимодействия в состоянии x достигает своего минимально возможного значения Eij= -(1/2) x ix jx ix j= -1/2.

При этом Е -полная энергия равна E = -(1/2) N 2, что отвечает глобальному минимуму.

Для запоминания других образов может применяется итерационный процесс:

который приводит к полной матрице связей в форме Хебба:

Устойчивость совокупности образов не столь очевидна, как в случае одного образа. Ряд исследований показывает, что нейронная сеть, обученная по правилу Хебба, может в среднем, при больших размерах сети N, хранить не более чем p » 0.14 N различных образов. Устойчивость может быть показана для совокупности ортогональных образов, когда

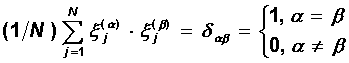
В этом случае для каждого состояния x aпроизведение суммарного входа i-го нейрона hiна величину его активности Si= x aiоказывается положительным, следовательно само состояние xa является состоянием притяжения (устойчивым аттрактором):

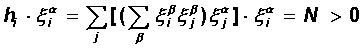
Таким образом, правило Хебба обеспечивает устойчивость сети Хопфилда на заданном наборе относительно небольшого числа ортогональных образов. В следующем пункте мы остановимся на особенностях памяти полученной нейронной сети.

1. Методы повышения эффективности обучения сети Хопфилда.

Сеть Хопфилда Сеть разработана Хопфилдом в 1984 году. С тех пор были предложены многочисленные модификации. Сеть используется как ассоциативная память, классификатор и для решения некоторых задач оптимизации. Одна из первых предложенных моделей сети Хопфилда используется как ассоциативная память. Исходными данными для расчета значений синаптических весов сети являются векторы - образцы классов. Сеть функционирует циклически. Выход каждого из нейронов подается на входы всех остальных нейронов. Нейроны сети имеют жесткие пороговые функции. Итерации сети завершаются после того, как выходные сигналы нейронов перестают меняться. Тип входных и выходных сигналов: биполярные (+1 и -1).

Размерности входных и выходных сигналов совпадают. Несколько слов о емкости сети Хопфилда: сеть, содержащая N нейронов может запомнить не более М=0.15 *N образов. При этом запоминаемые образы не должны быть сильно коррелированы.

Области применения: ассоциативная память, адресуемая по содержанию, задачи распознавания образов, задачи оптимизации.

Сеть обладает небольшой емкостью. Наряду с запомненными образами в сети хранятся и их негативы. Размерность и тип входных сигналов с точностью совпадают с размерностью и типом выходных сигналов. Это существенно ограничивает применение сети в задаче распознавания образов. При использовании коррелированных векторов-образцов возможно зацикливание сети в процессе функционирования.

Квадратичный рост числа синапсов при увеличении размерности входного сигнала также можно считать недостатком сети.

Сеть имеет огромное историческое значение. С этой модели началось возрождение интереса к нейронным сетям в середине 80-х годов.

Существует модель сети Хопфилда с бинарными входными сигналами.

Одна из модификаций сети предназначена для решения задач оптимизации, в частности задачи распределения работ между исполнителями.

Для увеличения емкости сети и повышения качества распознавания образов используют мультипликативные нейроны. Сети, состоящие из таких нейронов, называются сетями высших порядков.

Были предложены многослойные сети Хопфилда, которые обладают определенными преимуществами по сравнению с первоначальной моделью.

1. Сети Жордана. Структура. Принцип работы.(в 20)

1. Применение сетей Хопфилда. Пример.

Сеть Хопфилда может быть использована как ассоциативная память, для решения некоторых задач оптимизации, а также как фильтр (задачи распознавания образов).

Чтобы организовать устойчивую автоассоциативную память с помощью данной сети с обратными связями, веса должны выбираться так, чтобы образовывать энергетические минимумы в нужных вершинах единичного гиперкуба.

На каждом итерации алгоритма функционирования сети понижается значение энергии нейронной сети. Это позволяет решать комбинаторные задачи оптимизации, если они могут быть сформулированы как задачи минимизации энергии.

Рассмотрим пример восстановления повреждённого изображения.

Если во время обучения сформировать матрицу весовых коэффициентов на основании эталонных бинарных векторов, то нейронная сеть в процессе работы будет менять состояния нейронов до тех пор, пока не перейдет к одному из устойчивых состояний.

Пусть имеется нейронная сеть размерностью N=100 , в матрицу связей записан набор чёрно-белых картинок (-1 — чёрный цвет, +1 — белый), среди которых есть изображение собачки (рис. 3б). Если установить начальное состояние сети близким к этому вектору (рис. 3а), то в ходе динамики нейронная сеть восстановит исходное изображение (рис. 3б). В этом смысле можно говорить о том, что сеть Хопфилда решает задачу распознавания образов (хотя строго говоря, полученное эталонное изображение ещё нужно превратить в номер класса, что в некоторых случаях может быть весьма вычислительно ёмкой задачей).

а) б)

Рис. 3: а) начальное состояние для сети Хопфилда; б) восстановленное изображение.