
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет резерва методом неопределенных множителей Лагранжа и градиентным методом
Прежде всего для решения задачи оптимального резервирования используется метод неопределенных множеств Лагранжа:
Необходимо найти:


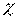
— неопределенный множитель Лагранжа;

— ограничение.
Решив систему уравнений, можно найти необходимое количество резервных элементов.

Метод не дает однозначного решения: аргументы будут нецелочисленными (надо округлять), ограничения заданы в виде строгого равенства, а надо больше или равно.
Для устранения указанных недостатков решения задачи оптимального резервирования используется градиентный метод.
Экстремум функции ищется из начальной точки по направлению градиента по шагам. Для оптимального резервирования на первом шаге отыскивается тот элемент системы, который дает наибольший прирост показателя надежности, на втором - элемент, у которого имеется максимальный прирост показателя надежности, включая уже зарезервированный, до тех пор, пока не выполниться ограничение (по стоимости). Метод называется покоординатным спуском, который является одним из самых простых методов поиска экстремума функции многих переменных (рис. 4.2).
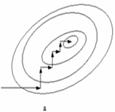 В литературе говориться, что данный метод может «застревать», когда линии уровня сильно вытянуты (см. рис. 4.2 б), т.е. пробные шаги во всех направлениях не приводят к уменьшению значения целевой функции, и процесс вычисления прерывается вдали от точки минимума.
В литературе говориться, что данный метод может «застревать», когда линии уровня сильно вытянуты (см. рис. 4.2 б), т.е. пробные шаги во всех направлениях не приводят к уменьшению значения целевой функции, и процесс вычисления прерывается вдали от точки минимума.

Рис. 4.2 Поиск минимума функции двух переменных методом покоординатного спуска
Но так как надо минимизировать функцию надежности системы

которая при всегда будет уменьшаться при увеличении количества резервных элементов, можно не усложнять алгоритм покоординатного спуска, например методом предложенным Хуком и Дживсом.
Дата добавления: 2015-01-19; просмотров: 285; Мы поможем в написании вашей работы!; Нарушение авторских прав |