Спутниковое нивелирование. Точность

Геодезическая высота некоторой точки является минимальным расстоянием между поверхностью эллипсоида и определяемой точкой. Совместно с плановыми координатами B, L геодезическая высота H определяет пространственное положение точки относительно заданного эллипсоида. Эти координаты называют эллипсоидальными. Геодезическая (эллипсоидальная) высота имеет только геометрический смысл и не может быть непосредственна измерена, поскольку в точке поверхности Земли неизвестны ни направление нормали к эллипсоиду, вдоль которой нужно измерять высоту, ни положение отсчетной точки на эллипсоиде, которая к тому же физически недоступна. Вычислить геодезические высоты или их разности (превышения) возможно по результатам спутниковых наблюдений, тригонометрического и астрономо-геодезического нивелирования.
Спутниковые методы позволяют определить пространственные прямоугольные координаты X, Y, Z точки. Эти координаты связаны с геодезическими формулами перехода. Спутниковое определение координат может осуществляться двумя методами: абсолютным, как правило, с точностью до 5 м или относительным, точность которого колеблется от первых дециметров до нескольких метров при кодовых измерениях и 3-10 мм при фазовых методах измерений. В абсолютном способе по измеренным величинам возможно вычислить значения геоцентрических координат, а в относительном методе по результатам измерений можно вычислить лишь приращения ΔX, ΔY, ΔZ пространственных координат. Наиболее эффективно проблема повышения точности решается за счет применения относительных методов спутниковых измерений.
Таким образом, самый распространенный на данный момент способ определения геодезических высот – это спутниковое нивелирование. До появления этой технологии, все высоты получали путем измерений на поверхности Земли. Полученные таким образом высоты носят название гипсометрических. Для связи гипсометрических и геодезических высот имеется соотношение H^г = H^гипс + ζ, где H^г – геодезическая высота точки, H^гипс – гипсометрическая высота (высота в физическом понимании), ζ – геоидальная составляющая высоты.

Нормальной высотой является высота над эллипсоидом в нормальном поле такой точки, для которой разность нормального потенциала относительно эллипсоида тождественно равна геопотенциальному числу точки поверхности Земли. Нормальные высоты практически не зависят от выбора эллипсоида и определяются по результатам измерений, выполненных на физической поверхности Земли. Однако они связаны с выбором начальной точки, от которой выполняется геометрическое нивелирование и ведется счет геопотенциальных чисел. В России отсчет высот принято вести от нуль-пункта Кронштадского футштока. Нормальная система высот выгодно отличается от ортометрической тем, что не требует гипотез о распределении масс внутри Земли, поэтому вычислить значение высоты можно достаточно точно, а качество полученных высот зависит в основном только от качества измерений. Нормальные высоты могут быть определены из результатов нивелирования, а также вычислены по геодезическим высотам, если есть информация о разностях (Н^г – Н^γ), то есть высотах квазигеоида ζ, поскольку сумма нормальной высоты и аномалии высоты дает геодезическую высоту точки поверхностиЗемли: Н^г =Н^γ+ζ.
Аномалия высоты возникает из-за того, что гравитационное поле Земли не совпадает с нормальным, поэтому нормальная высота Н^γ не равна геодезическойН^г. Поскольку нормальный потенциал всегда выбирают близким к действительному, аномалия высоты будет сравнительно малой величиной. Если отложить нормальные высоты по нормали к эллипсоиду от каждой точки поверхности Земли с учетом знака высоты вниз или вверх, то геометрическое место точек концов этих отрезков образуют поверхность, которую называют квазигеоидом. Следовательно, высота квазигеоида над эллипсоидом равна аномалии высоты.
При использовании спутниковых измерений нет необходимости связывать начало счета нормальных высот с потенциалом на уровне моря. В этом случае нормальные высоты полностью определены выбором эллипсоида и потенциалом реальной Земли. В основе всех методов определения координат пунктов наблюдения с использованием глобальной навигационной спутниковой системы лежит метод засечки положения мобильного приемника от известных положений навигационного космического аппарата. Определение относительных координат по спутниковым измерениям может быть выполнено дифференциальным или относительным методом.
Дифференциальный режим реализуется с помощью контрольного спутникового приёмника, называемого опорной станцией. В этом методе по результатам наблюдений на опорном пункте формируются дифференциальные поправки к соответствующим параметрам наблюдений для определяемого пункта, т.е. наблюдения на опорном пункте и пункте наблюдения обрабатываются раздельно. Этот метод обеспечивает решения в реальном масштабе времени. Метод определения относительных координат по кодовым псевдодальностям в настоящее время обеспечивает точность 3-5 м, по фазовым измерениям может достигать средней квадратической ошибки, равной 1 мм.
В относительном методе наблюдения, выполненные одновременно на опорном и определяемом пункте, обрабатываются совместно, что исключает высокоточные мгновенные решения.
Одним из методов спутникового нивелирования является спутниковая альтиметрия, под которой понимается измерение высоты спутника относительно поверхности Земли по времени прохождения сигнала. Спутниковое нивелирование и спутниковую альтиметрию объединяет то, что в обоих методах по результатам измерений необходимо вычислять геодезические и нормальные высоты объекта наблюдения. Суть этого метода заключается в следующем. Радиовысотомер, установленный на борту ИСЗ, измеряет высоту мгновенного положения ИСЗ над средним уровнем океана. Отраженный сигнал в идеальных условиях прохождения тем же кратчайшим путем возвращается в приемник радиовысотомера. Если на моменты измерения высот спутниковым радиовысотомером вычислять геодезические координаты мгновенных положений ИСЗ, то возможно для некоторой площадки геоида определить высоту геоида над эллипсоидом. Отклонения (положительные или отрицательные) геоида относительно эллипсоида называют ондуляциями геоида.
Метод спутниковой альтиметрии позволяет уточнить параметры грави-тационного поля Земли, положение начала системы координат относительно центра масс Земли и получить уравнение геоида, то есть уточнить форму морского геоида.

можно представить в виде, удобном для вычисления геодезической высоты через декартовы координаты

Для оценки точности вычисления геодезической высоты по результатам спутниковых измерений формула (8) представлена в следующем виде:
, (9)

где - радиус кривизны первого вертикала, выраженный через прямоугольные координаты; . (10)

Полный дифференциал выражения (8) имеет вид:

. (11)

Для оценки точности вычисления разности геодезических высот по результатам спутниковых измерений в соответствии с принятыми обозначениями и формулой (9), можно записать:

, (20)

где ;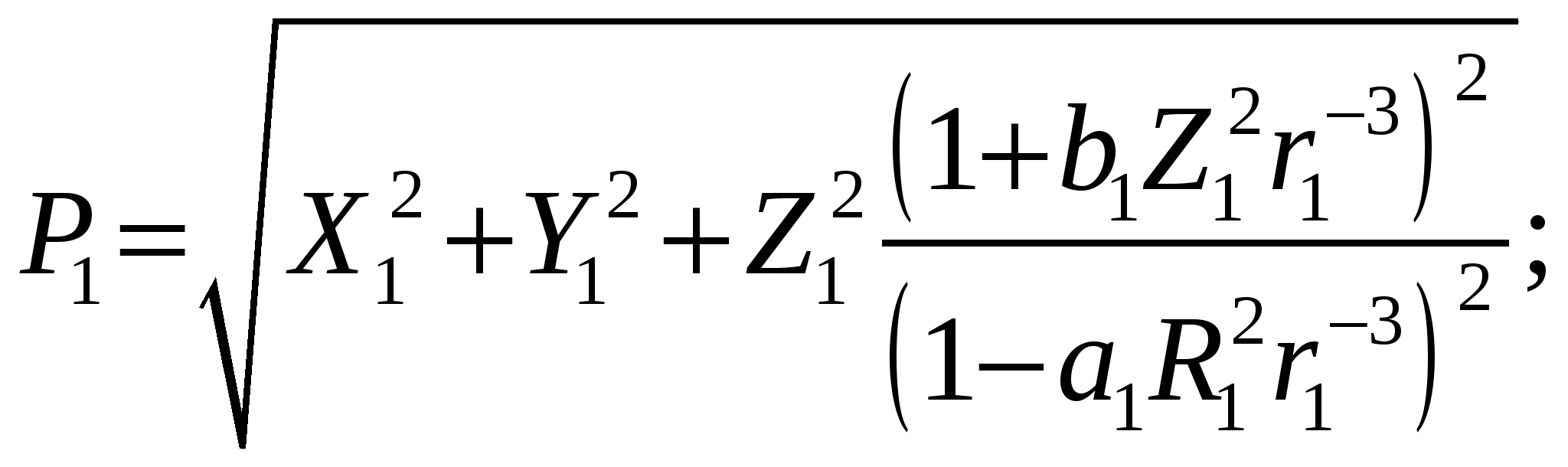

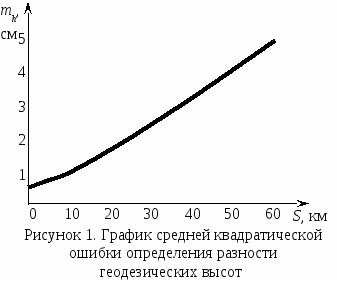
Приведенный анализ точности показал, что при вычислении разности геодезических высот существенное влияние оказывает ошибка координат опорного пункта. Средняя квадратическая ошибка определения координат опорного пункта в среднем равна 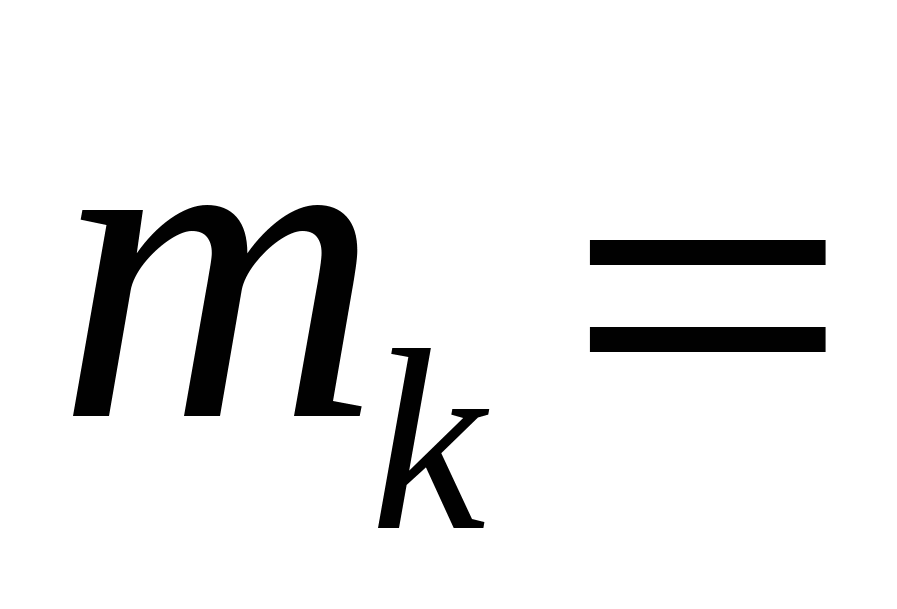5 м, а сре-дняя квадратическая ошибка определения приращений координат = 5 мм.