Образец решения примеров.

Пример 1.Найти пределы функций.

1) .

2) .

3)

4)

.

5) 6)

7)

8) .

При решении использовали первый специальный предел и теоремы о применении эквивалентных бесконечно малых в пределах.

Пример 2.Вычислить производные функций.

1)

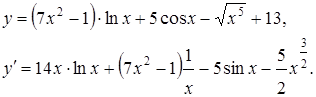
2)

3)

Зависимость между переменными и задана параметрическими уравнениями. Искомая производная определяется по формуле . Имеем:

Откуда

4) Найти производную функции y, если .

Дифференцируем обе части данного уравнения по , считая функцией от :

.

Отсюда находим

.

Пример 3. Найти наибольшее и наименьшее значения функции

на отрезке .

Общая схема исследования:

1) найти критические точки, лежащие внутри отрезка ;

2) вычислить значения на концах отрезка, то есть найти и ;

3) сравнив найденные значения со значениями функции в критических точках, выбрать наибольшее и наименьшее;

Найдем сначала критические точки, принадлежащие интервалу :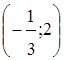

.

Теперь вычислим значения заданной функции в критических точках и на концах отрезка:

Сравнивая полученные значения функции, заключаем, что

Пример 4.Найти все частные производные первого порядка функции двух переменных .

При вычислении частной производной по « x », « y» считаем постоянной. Аналогично, при нахождении частной производной по « y », считаем постоянной « x ».

;

.