Матрицы, определители, системы уравнений

Пример 1. . Найти .

Решение.

.

.

Пример 2. .Найти произведение матриц.

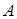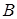Решение. Матрица имеет размерность , а матрица - размерность . Имеет смысл только произведение , причем в результате перемножения матриц получается матрица размерности :

.

Пример 3.Решить систему линейных уравнений по формулам Крамера:

Решение. Решение системы линейных уравнений с невырожденной квадратной матрицей определяется по формулам Крамера .

Найдем все определители, входящие в формулы Крамера, разложением по элементам первой строки:

,

,

.

Значит, - решение данной системы.

Пример 4.Решить систему линейных уравнений методом Гаусса:

Решение. Выполним прямой ход метода Гаусса: составим расширенную матрицу системы и путем элементарных преобразований строк приведем ее к эквивалентной матрице ступенчатого вида:

Выполним обратный ход метода Гаусса, составив по ступенчатой матрице систему линейных уравнений:

.

Пример 5.Определим матрицу, обратную матрице . Решение. Такая матрица существует, так как соответствующий ей определитель не равен нулю. Найдем алгебраические дополнения

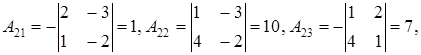
Теперь транспонируем матрицу, составленную из алгебраических дополнений, и разделим ее элементы на 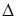, тогда обратная матрица

.