Симметричная трехфазная цепь при соединении звездой и треугольником векторные диаграммы

Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению Z_A = Z_B = Z_C = R.
Узловое напряжение

,

потому что трехфазная система ЭДС симметрична, .

Напряжения фаз нагрузки и генератора одинаковы:

Фазные токи одинаковы по величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует

В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.

Соединение «звездой»

На рис. 7.7 показано соединение нагрузки «звездой» с нейтральным проводом.

Рис. 7.7. Соединение нагрузки «звездой» с нейтральным проводом

Рис. 7.8. Векторная диаграмма при активно-индуктивной нагрузке

К каждой фазе приемника прикладывается соответствующее напряжение источника. Напряжения источника образуют симметричную систему векторов. Так как Z_a = Z_b = Z_c = Z, то каждый из векторов токов сдвинут относительно фазного напряжения на один и тот же угол j, и, следовательно, векторы фазных токов также образуют симметричную систему. Если сопротивления приемника носят активно-индуктивный характер (j > 0), то векторная диаграмма токов и напряжений имеет следующий вид (рис. 7.8).

Ток в нейтральном проводе будет равен нулю:

I_N = I_A + I_B + I_C = 0.

В этом можно убедиться, если просуммировать проекции векторов токов на действительную и мнимую оси. Отсутствие тока в нулевом проводе делает его не нужным. Поэтому для симметричных приемников можно не применять нулевой провод.

Линейные напряжения определяются как разность фазных напряжений

(7.4)

Рис. 7.9. Топографическая диаграмма напряжений

Топографическая диаграмма напряжений имеет вид, показанный на рис. 7.9.

Рассматривая треугольник ANB и учитывая, что U_A = U_B = U_C = U_ф и U_AB = U_BC = U_CA = U_л, будем иметь

.

Линейные и фазные токи равны друг другу. Следовательно, в симметричной трехфазной системе: .

К каждой фазе приемника с сопротивлением Zab = Zbc = Zca = Z прикладывается линейное напряжение источника (рис. 7.10). Векторная диаграмма напряжений образует звезду. Причем линейные напряжения равны фазным Uab = Ubc = Uca = Uл = UФ. Фазные токи сдвинуты относительно соответствующих напряжений на угол j. Линейные токи в соответствии с первым законом Кирхгофа определяются как разность фазных токов: (7.5) Из этой системы следует, что сумма линейных токов т.е. на векторной диаграмме они образуют замкнутый треугольник токов. Рис. 7.10. Соединение нагрузки «треугольником» 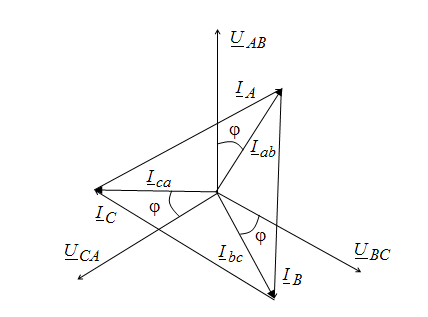Рис. 7.11. Векторная диаграмма токов и напряжений при соединении нагрузки «треугольником» Для активно-индуктивной нагрузки (j > 0) векторная диаграмма имеет вид, показанный на рис. 7.11. Так как линейные токи образуют равносторонний треугольник, то фазные и линейные токи находятся в соотношении . Таким образом, в симметричной трехфазной цепи при соединении «треугольником» имеем соотношение UФ = Uл;Iл = . В целом необходимо отметить, что сумма линейных напряжений (всегда) и сумма линейных токов (в трехпроводной цепи) равны нулю.