
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Логические операции
Основные логические операции над высказываниями, используемыми в ЭВМ, включают отрицание, конъюнкцию, дизъюнкции, стрелку Пирса и штрих Шеффера. Рассмотрим эти логические операции.
1. Отрицание 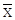 (обозначается также ØX, ~X).
(обозначается также ØX, ~X).
Отрицание 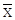 (NOT, читается «не X») – это высказывание, которое истинно, если X ложно, и ложно, если X истинно.
(NOT, читается «не X») – это высказывание, которое истинно, если X ложно, и ложно, если X истинно.
2. Конъюнкция XY (X&Y, XÙY).
Конъюнкция XY (AND, логическое умножение, «X и Y») – это высказывание, которое истинно только в том случае, если X истинно и Y истинно.
3. Дизъюнкция X+Y (XÚY).
Дизъюнкция X+Y (OR, логическая сумма, «X или Y или оба») – это высказывание, которое ложно только в том случае, если X ложно и Y ложно.
4. Стрелка Пирса X ¯ Y.
Стрелка Пирса X ¯ Y (NOR (NOT OR), ИЛИ-НЕ) – это высказывание, которое истинно только в том случае, если X ложно и Y ложно.
5. Штрих Шеффера X | Y.
Штрих Шеффера X | Y (NAND (NOT AND), И-НЕ) – это высказывание, которое ложно только в том случае, если X истинно и Y истинно.
Определить значения логических операций при различных сочетаниях аргументов можно из таблицы истинности.
Таблица истинности для основных логических операций, используемых в ЭВМ
| X | Y | 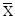
| XY | X + Y | X ¯ Y | X | Y |
Чтобы определить значение операции 0 + 1 в таблице истинности, необходимо на пересечении столбца X + Y (определяет операцию) и строки, где X = 0 и Y = 1 (так первый аргумент равен 0, а второй – 1), найти значение 1, которое и будет являться значением операции 0 + 1.
В алгебре высказываний существуют две нормальные формы: конъюнктивная нормальная форма (КНФ) и дизъюнктивная нормальная форма (ДНФ).
КНФ – это конъюнкция конечного числа дизъюнкций нескольких переменных или их отрицаний (произведение сумм). Например, формула X(Y + Z) находится в КНФ.
ДНФ – это дизъюнкция конечного числа конъюнкций нескольких переменных или их отрицаний (сумма произведений). Например, формула X + YZ находится в ДНФ.
Логические операции обладают свойствами, сформулированными в виде равносильных формул.
Снятие двойного отрицания (отрицание отрицания):
 =X. (6.1)
Коммутативность:
XY=YX. (6.2)
X+Y=Y+X. (6.3)
Ассоциативность:
(XY)Z=X(YZ). (6.4)
(X+Y)+Z=X+(Y+Z). (6.5)
Дистрибутивность:
X(Y+Z)=XY+XZ. (6.6)
X+YZ=(X+Y)(X+Z). (6.7)
Законы де Моргана: =X. (6.1)
Коммутативность:
XY=YX. (6.2)
X+Y=Y+X. (6.3)
Ассоциативность:
(XY)Z=X(YZ). (6.4)
(X+Y)+Z=X+(Y+Z). (6.5)
Дистрибутивность:
X(Y+Z)=XY+XZ. (6.6)
X+YZ=(X+Y)(X+Z). (6.7)
Законы де Моргана:
 . (6.8) . (6.8)
 . (6.9)
Идемпотентность:
X+X=X. (6.10)
X×X=X. (6.11)
Закон противоречия:
X× . (6.9)
Идемпотентность:
X+X=X. (6.10)
X×X=X. (6.11)
Закон противоречия:
X×  =0. (6.12) =0. (6.12)
| Закон «исключения третьего»:
X+  =1. (6.13)
Свойства констант:
X×1=X. (6.14)
X×0=0. (6.15)
X+1=1. (6.16)
X+0=X. (6.17)
Элементарные поглощения:
X+XY=X. (6.18)
X+ =1. (6.13)
Свойства констант:
X×1=X. (6.14)
X×0=0. (6.15)
X+1=1. (6.16)
X+0=X. (6.17)
Элементарные поглощения:
X+XY=X. (6.18)
X+  Y=X+Y. (6.19)
X(X+Y)=X. (6.20)
X( Y=X+Y. (6.19)
X(X+Y)=X. (6.20)
X(  +Y)=XY. (6.21)
Преобразование стрелки Пирса:
X¯Y= +Y)=XY. (6.21)
Преобразование стрелки Пирса:
X¯Y= 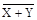 . (6.22)
Преобразование штриха Шеффера:
X | Y= . (6.22)
Преобразование штриха Шеффера:
X | Y= 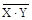 . (6.23) . (6.23)
|
Порядок применения формул при преобразованиях - перечисленные формулы рекомендуется применять в следующем порядке:
1) преобразование стрелки Пирса (6.22) и штриха Шеффера (6.23);
2) законы де Моргана (6.8)-(6.9);
3) формулы дистрибутивности (6.6)-(6.7);
4) элементарные поглощения (6.18)-(6.21).
Обычно формула приводится к ДНФ, а затем отдельные слагаемые поглощаются.
Дата добавления: 2015-01-29; просмотров: 286; Мы поможем в написании вашей работы!; Нарушение авторских прав |