
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример расчета нейтронограммы ядерного рассеяния
Пусть соединение AB имеет объемноцентрированную кубическую решетку, и пусть атомы сорта A занимают углы куба, а атомы сорта B расположены в центре куба:

Тогда атом A имеет координаты (0, 0, 0), а атом B - координаты (½, ½, ½). Пусть параметр решетки соединения AB равен a = 4 Ǻ. Примем, что амплитуда когерентного рассеяния атомами сорта A равнаs bA = 1·10-12 cm, а атомами сорта B - bB = -1·10-12 cm.
Давайте рассчитаем нейтронограмму для этого соединения.
Пусть падающий пучок нейтронов имеет длину волны l = 2 Ǻ, образец представляет собой пластинку, полностью перекрывающую пучок.
Выпишем еще раз формулы для интенсивностей ядерных рефлексов:
I(hkl) =  l3×j(hkl) × F2(hkl)× LA(hkl)×T(hkl)×y-1/2×R(hkl)×dV, (2.34)
l3×j(hkl) × F2(hkl)× LA(hkl)×T(hkl)×y-1/2×R(hkl)×dV, (2.34)
F2(hkl) = A2(hkl) + B2(hkl), (2.35)
A(hkl) =  , (2.36)
, (2.36)
B(hkl) =  . (2.37)
. (2.37)
Для простоты рассмотрим случай, когда интенсивность падающего пучка, скорость сканирования и объем образца в пучке постоянны. Будем пренебрегать экстинкцией. Пусть также, атомы A и B не обладают аномально большим поглощением.
Тогда формулу (2.34) можно записать в виде:
I(hkl) = S·L(hkl)·j(hkl)·F2(hkl)·T(hkl) (2.38)
где S масштабный множитель.
В случае кубической структуры следующие рефлексы возможны: (100), (110), (111), (200), (210), и т.д.
Рассчитаем структурные факторы этих рефлексов.
(100)
F2100 = A2100 + B2100
A100 =  ·cos2p(1·xn + 0·yn + 0·zn) =
·cos2p(1·xn + 0·yn + 0·zn) =
= 1·cos2p(1·1 + 0·0 + 0·0) + (-1)·cos2p(1·½ +0·½ + 0·½) =
= 1·cos2p(0) + (-1)·cos2p(½) = 1·1 + (-1)· (-1) = 2.
A2100 = 22 = 4.
B2100 = 0.
Следовательно, F2100 = A2100 = 4. (2.38)
Рассчитаем структурный фактор F2101 для (101) рефлекса.
A101 = 1·cos2p(1·1 + 0·0 + 1·0) + (-1)·cos2p(1·½ +0·½ + 1·½) =
= 1·1 + (-1)·1 = 0.
B101 = 0.
Итак, F2101 = 0. (2.39)
В случае (111) рефлекса:
A111 = 1·cos2p(1·1 + 1·0 + 1·0) + (-1)·cos2p(1·½ +1·½ + 1·½) =
= 1·cos2p(3) + (-1)·cos2p(1½) = 1·1 + (-1)· (-1) = 2.
A2111 = 4.
B2111 = 0.
F2111 = A2111 = 4. (2.40)
Рассчитаем фактор Лоренца (случай пластинки):
Lhkl = 1/sin22Qhkl. (2.41)
Чтобы определить угловые положения рефлексов, воспользуемся формулой Вульфа-Брегга:
sinQhkl = l/2dhkl, (2.42)
где,
dhkl = a/  , (2.43)
, (2.43)
Итак,
sinQhkl = l  /2a.
/2a.
Следовательно, угловые позиции рефлексов (100) и (111):
sinQ100 = 2  /2·4 = ¼ , Q100 = 14.5°, 2Q100 = 29.0° (2.44)
/2·4 = ¼ , Q100 = 14.5°, 2Q100 = 29.0° (2.44)
sinQ111 = 2  /2·4 = √3/4, Q111 = 25.6°, 2Q111 = 51.2° . (2.45)
/2·4 = √3/4, Q111 = 25.6°, 2Q111 = 51.2° . (2.45)
Тогда,
L100 = 1/sin229.0° = 4.255, (2.46)
L111 = 1/ sin297.2° = 1.016. (2.47)
Рассчитаем фактор повторяемости jhkl для (100) и (111).
Возможные перестановки для (100):100, -100, 010, 0-10, 001, 00-1.
Следовательно, j(100) = 6.
Возможные перестановки для (111):111, -1-1-1, 1-1-1, -111, 1-11, -11-1, 11-1, -1-11.
Итак, j(111) = 8.
Рассчитаем интенсивности рефлексов (100) и (111).
I(100) = 6´4.255´4 = 102.12 (барн), (2.48)
I(111) = 8´1.016´4 = 32.51 (барн). (2.49)
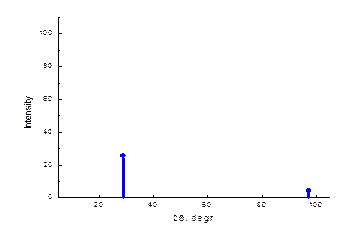
Если не учитывать функцию разрешения дифрактометра, то можно представить наши результаты в виде следующей нейтронограммы соединения. AB.

Рассчитаем поправку на поглощение.
Thkl = exp (-mt)secQhkl (2.50)
Для многокомпонентного образца обычно используют массовый коэффициент поглощения:
msample = rsample[c1(m1/r1) + c2(m2/r2) + ...+ cn(mn/rn)], (2.51)
где, msample и rsample – линейный коэффициент поглощения образца и его плотность, ci - концентрация i-компоненты в образце в массовых %.
Пусть rsample = 5 g/cm3; mA/rA = 2 cm2/g-1; mB/rB = 0.2 cm2/g-1; cA = 0.734, cB= 0.266.
Тогда,
msample = 5[(0.734´2) + (0.266´0.2)] = 7.6 (cm-1).
Пусть толщина образца t = 2 mm = 0.2 cm, тогда поправка на поглощение равна
T100 = exp(-7.6´0.2´sec14.5°) = exp(-1.57) = 0.25.
T111 = exp(-7.6´0.2´sec48.6°) = exp(-2.3) = 0.13.
Как можно видеть, поправка на поглощение достаточно большая. Принимая во внимание поправку на поглощение, уточним вид нашей расчетной нейтронограммы.
Дата добавления: 2015-01-29; просмотров: 212; Мы поможем в написании вашей работы!; Нарушение авторских прав |