Материальный баланс массообменных процессов

Материальный баланс характеризует статику массопередачи и служит для установления математической зависимости между потоками веществ, взаимодействующих в массообменном аппарате.

Пусть в массообменном аппарате взаимодействуют 2 фазы. 1-я – газовая, проходит через аппарат снизу вверх, расход её 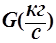; (имеется в виду инертная часть газа). 2-я – жидкость, .

Начальные концентрации распределяемого между фазами вещества и условия равновесия таковы, что массопередача осуществляется из фазыGв фазу L; причем - начальная и конечная концентрации распределяемого вещества в фазе G, - начальная и конечная концентрация распределяемого вещества в фазе L.( Здесь концентрации y и x - относительные, т.е. , при этом абсолютные количества инертного вещества в каждой фазе G и Lне изменяются по высоте аппарата (т.е. G,L= const).

G, L,

Схема материальных потоков

в массообменном аппарате.

a у х b

-dy dx

G, L,

Выделим в аппарате 2-мя // плоскостями 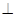к направлению движения потоков бесконечно малый участок фазового контакта. На этом участке концентрация распределяемого вещества в фазе G уменьшается на величину dy, а в фазе L увеличивается на величину dx. Таким образом, количество перешедшего вещества из G в L на этом участке равно:

dM = - Gdy = Ldx (а) дифференциальное уравнение материального баланса. Проинтегрируем это выражение в пределах всего аппарата

M = G(y_H-y_K)=L(x_K-x_H) – уравнение материального баланса массообменного аппарата. Это уравнение дает возможность определить соотношения между материальными потоками в аппарате. Например, расходы фаз:

и

Если проинтегрировать уравнение (а) в пределах от низа аппарата до произвольного сечения a-b (где концентрации фаз у и х), получим:

; решим относительно у

. (*)

Выражение (*) является уравнением прямой линии, где 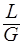- удельный расход одной из фаз.

Уравнение (*) называется уравнением рабочей линии. Оно устанавливает связь между концентрациями распределяемого вещества (y,x), которые называются рабочими концентрациями во взаимодействующих фазах. В координатах y-x эта зависимость выражается прямой, крайние точки которой определяются концентрациями вверху и внизу аппарата (см.рис.)

График рабочей линии процесса