
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средняя интегральная разность концентраций.
Если равновесная кривая не является линейной, то средняя движущая сила вычисляется как средняя интегральная разность концентраций и определяется следующим образом. Запишем дифференциальное уравнение материального баланса для фазы G и уравнение массопередачи для элемента поверхности dF  и
и  , откуда
, откуда  . Интегрируя в пределах O-F,
. Интегрируя в пределах O-F, 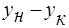 , получим при
, получим при 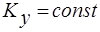

 .
.
Значение  находится методом графического интегрирования. Для этого берется ряд значений x (см. рис. ), находятся соответствующие значения
находится методом графического интегрирования. Для этого берется ряд значений x (см. рис. ), находятся соответствующие значения 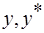 и вычисляются величины
и вычисляются величины  , строится зависимость
, строится зависимость  . (рис). Значение интеграла будет равно площади S, умноженной на масштаб a, тогда:
. (рис). Значение интеграла будет равно площади S, умноженной на масштаб a, тогда:
 . Из уравнения
. Из уравнения 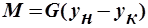 выразим G и подставим
выразим G и подставим 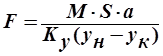 , или
, или  (**)
(**)








 Графическое определение
Графическое определение


S
 |
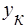
 y
y
Сравним (**) с (ОУМП). Видно, что 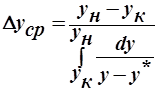 ( получили выражение для среднеинтегральной движущей силы.)
( получили выражение для среднеинтегральной движущей силы.)
Записав дифференциальное уравнение материального баланса и уравнение массопередачи для фазы L, аналогично найдем:
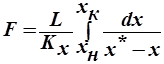 , при
, при 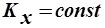 и
и  .
.
Дата добавления: 2015-01-29; просмотров: 247; Мы поможем в написании вашей работы!; Нарушение авторских прав |