Интенсивность испарения влаги

; гдеW – количество влаги; F – поверхность материала; – время сушки,

m – интенсивность испарения влаги - связана с механизмом теплообмена влажного материала с окружающей средой. Процесс очень сложный и состоит из стадий перемещения влаги из глубины материала к поверхности и от поверхности в окружающую среду.

Испарение влаги с поверхности материала. Процесс происходит вследствие диффузии пара через пограничный слой воздуха у поверхности материала (внешняя диффузия). Процесс обусловлен движущей силой – разностью концентраций или парциальных давлений пара у поверхности и в окружающей среде. Кроме того, существует мольный перенос и термодиффузия (из-за перепада температур).

Перемещение влаги внутри материала. При испарении влаги с поверхности материала внутри материала возникает градиент влажности, в результате чего происходит перемещение влаги из глубины. В I период влажность внутри велика, лимитирующей стадией является скорость поверхностного испарения (внешняя диффузия). На II периоде лимитирующей стадией становится внутренняя диффузия. Перенос влаги внутри материала называется влагопроводностью. Интенсивность потока влаги пропорциональна градиенту концентрации влаги ; . (Минус, т.к. влага движется от большей к меньшей концентрации). k – коэффициент влагопроводности, зависящий от формы связи влаги с материалом, влажности материала, температуры сушки, определяется экспериментальным путём.

Скорость уменьшения влажности материала может быть выражена общим дифференциальным уравнением влагообмена: , где δ – коэффициент термовлагопроводности; 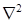- оператор Лапласа.

В случае одномерной задачи: 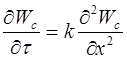. Зная закон распределения влажности в материале в начале сушки и выражение для плотности потока влаги с поверхности материала окружающую среду это дифференциальное уравнение можно решить. Интегрируя, получаем: ; где: N – скорость сушки; - начальная и первая критическая влажности; τ_К1 – время сушки за весь первый период. Это уравнение является уравнением прямой ВС на кривой сушки. Продолжительность периода первой стадии сушки: .

Продолжительность сушки на стадии падающей скорости определить сложнее из-за сложности конфигурационных кривых скорости сушки. Продолжительность сушки здесь определяют с помощью коэффициента скорости сушки k_С. Для расчёта k_С используют экспериментальную кривую скорости сушки для материала.

Уравнение скорости сушки для второго периода . Интегрируя это уравнение можно получить продолжительность сушки за II период. Существуют и другие методы расчётов продолжительности сушки (эмпирические). Их общий недостаток – они пригодны только для тех условий и материалов для которых получены.