Регулярные выражения

Определим следующие операции над множествами:

·

·

·

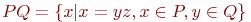
Тогда регулярные выражения над алфавитом T и языки, представляемые ими, могут быть определены следующим образом:

· Символ 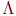, представляющий пустое множество, является регулярным выражением.

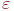· является регулярным выражением и представляет множество .

· Для каждого символа 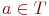a является регулярным выражением и представляет множество {a}.

· Если p и q - регулярные выражения, представляющие множества P и Q , то (pq) , (p+q) и (p*) являются регулярными выражениями, представляющими множества PQ, 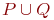и P* соответственно.

Отметим, что в этом определении подразумевается следующая система приоритетов: знак * обладает наивысшим приоритетом, за ним следует символ конкатенации, за которым следует символ |. Приоритеты можно изменять с помощью использования скобок.

Пример. Регулярное выражение 1(0+1)*1+1 представляет множество цепочек, начинающихся и заканчивающихся символом 1.

Упомянем без доказательства, что регулярные выражения эквивалентны праволинейным грамматикам. Таким образом, регулярным выражениям также соответствует естественный класс распознавателей в виде конечных автоматов.

Пример. Рассмотренная выше грамматика для идентификатора может быть записана с помощью следующего регулярного выражения: Letter (Letter | Digit)*.