LL(1) - грамматики

Наиболее просто данный анализатор строится для LL(1) грамматики. Таблица анализа для данной грамматики не имеет множественных записей. L – просмотр входного потока слева направо, L – левое порождение (вывод), (1) – просмотр одного символа из входного потока на каждом шаге для принятия решения о дальнейшем действие.

Примечание: имеются грамматики, которые нельзя привести к LL(1).

Пример:

Построим анализатор, работающий с грамматикой LL(1).

Имеется грамматика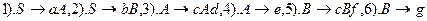

и цепочка: .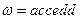

Конфигурация, описывающая состояние анализатора в общем ви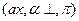де: , где 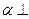- содержимое магазина; 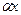- необработанная часть цепочки (a - текущий символ); - построенный к данному моменту разбор.

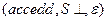
1) Из S порождаем цепочку. Так как первым в является символ a, то используем продукцию 1). Получаем: .

2) В вершине магазина находится терменальный символ a. Так как он совпадает с первым символом 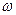, можно его вычеркнуть и продолжить анализ ( ).

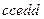3) Текущий символ входной цепочки – c. В вершине магазина - A, поэтому выбираем правило 3). Таким образом получим: .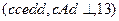

Дальнейший анализ заполнен в таблице:

№ шага	Входная цепочка	Магазин	Действие
вычеркнутое	оставшееся
		accedd	S	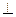правило 1).
		accedd	aA	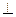вычеркнуть a
	a	ccedd	A	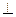правило 3).
	a	ccedd	cAd	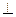вычеркнуть c
	ac	cedd	Ad	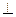правило 3).
	ac	cedd	cAdd	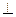вычеркнуть c
	acc	edd	Add	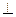правило 4).
	acc	edd	edd	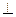вычеркнуть e
	acce	dd	dd	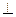вычеркнуть d
	acced	d	d	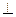вычеркнуть d
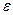
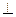
	accedd			цепочка допускается

КС – грамматика без 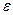– правил называется простой LL(1) (или S – грамматикой или разделенной грамматикой), если 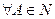все его альтернативы начинаются различными терминальными символами.

Введем ряд определений:

FIRST (A) – это множество терменальных символов, которыми начинаются цепочки, выводимые из терминала A:

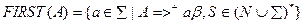
FOLLOW (A) – это множество терменальных символов, которые могут встретиться непосредственно справа от нетерменала A в некоторой цепочке:

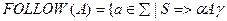и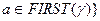

Пример:

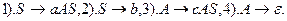
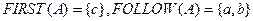
SELECT – это множество выбора правил. Оно определяется:

1) eсли 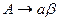, то ;

2) если 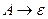, то .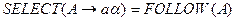

LL(k) – грамматика.

КС – грамматика является LL(1), тогда и только тогда, когда для двух различных правил A→β, А→γ 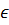Р пересечение при всех таких wАα, что S 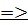* wАα.

Мощности LL(1)-грамматик недостаточно, чтобы описать синтаксис любых языков программы. Естественным обобщением LL(1)-грамматик является LL(k) – грамматика. Для этого введем обобщение множеств FIRST(α) множество 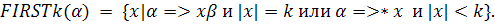Оно представляет собой множество терминальных префиксов длины k терминальных цепочек, выводимых из α (или меньшей длины, если выводимые цепочки меньше k). Аналогично определяем FOLLOW_k(A).

LL(k) применяются на практике редко из-за сложности.