
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предсказывающий алгоритм разбора.
Работой алгоритма управляет управляющая таблица M, которая задает отображение множества 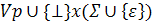 множество, состоящее из следующих элементов:
множество, состоящее из следующих элементов:
1) (β,i), β 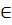 Vp*, (Vp – это алфавит магазинных символов без символа дна ⊥); β – правая часть правила вывода с номером i;
Vp*, (Vp – это алфавит магазинных символов без символа дна ⊥); β – правая часть правила вывода с номером i;
2) “Выброс”. В этом случае удаляется верхний символ магазина, читающая головка сдвигается на один символ вправо, выходная лента не изменяется.
3) Может быть слово “Допуск” . В этом случае значение в таблице должно иметь вид: пустой магазин, пустая строка M(⊥,ε).
4) Ошибка – в таблице ячейка ничем не заполняется.
Пример:
Есть грамматики :
1) E→TE’
2) E’→+TE’
3) E’→ε
4) T→PT’
5) T’→*PT’
6) T’→ε
7) P→(E)
8) P→i
Таблица строится так:
Имеется 11 строк: {N 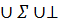 }={E,E’,T,T’,P,+,*,i,(,),⊥};
}={E,E’,T,T’,P,+,*,i,(,),⊥};
Имеется 6 столбцов: {i,(,),+,*,ε}=Σ 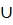 ε
ε
| i | ( | ) | + | * | ε | |
| E | TE’,1 | TE’,1 | ||||
| E’ | ε,3 | +TE’,2 | ε ,3 | |||
| T | PT’,4 | PT’,4 | ||||
| T’ | ε,6 | ε,6 | *PT’,5 | ε,6 | ||
| P | i,8 | (E),7 | ||||
| i | Выброс | |||||
| ( | В | |||||
| ) | В | |||||
| + | В | |||||
| * | В | |||||
| Допуск |
1) E→TE’
Последовательно расссмотрим все нетерминалы, т.к. FIRST(TE’)={(,i}
M(E,()=M(E,i)=(TE’,1)
2) E’→+TE’; FIRST(+TE’)={+}
M(E’,+)=(+TE’,2)
3) E’→ε, в этом случае пустая правая часть, нужно вычислить множество символов, следующих за нетерминалом E’ в выражениях, построив левый вывод, т.е.:
E 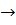 TE’
TE’ 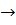 PT’E’→(E)T’E’→(TE’)TE’…
PT’E’→(E)T’E’→(TE’)TE’…
FOLLOW (E’)={),ε}
M(E’,))=M[E’,3]=(ε,3)
и т. д.
M(⊥,E) – допуск.
По данной таблице необходимо провести пошаговую проверку работы:
Будем проверять цепочку: i+i*i
Начальная конфигурация (i+i*i, E, ε )
Первая конфигурация: (i+i*i, TE’, 1 )
Получаем: (i+i*i, PT’E’,14 )
Проанализировать таблицу и получить допуск.
Дата добавления: 2015-01-29; просмотров: 261; Мы поможем в написании вашей работы!; Нарушение авторских прав |