Прикладные аспекты моделирования

Рассмотрим клеточно-автоматную модель загрязнения среды, диффузии загрязнителя в некоторой среде. 2D - клеточный автомат (на плоскости) для моделирования загрязнения среды может быть сгенерирован следующими правилами:

· плоскость разбивается на одинаковые клетки: каждая клетка может находиться в одном из двух состояний: состояние 1 - в ней есть диффундирующая частица загрязнителя, и состояние 0 - если ее нет;

· клеточное поле разбивается на блоки 2×2 двумя способами, которые будем называть четным и нечетным разбиениями (у чётного разбиения в кластере или блоке находится четное число точек или клеток поля, у нечетного блока - их нечетное число);

· на очередном шаге эволюции каждый блок четного разбиения поворачивается (по задаваемому правилу распространения загрязнения или генерируемому распределению случайных чисел) на заданный угол (направление поворота выбирается генератором случайных чисел);

· аналогичное правило определяется и для блоков нечетного разбиения;

· процесс продолжается до некоторого момента или до очищения среды.

Пусть единица времени - шаг клеточного автомата, единица длины - размер его клетки. Если перебрать всевозможные сочетания поворотов блоков четного и нечетного разбиения, то видим, что за один шаг частица может переместиться вдоль каждой из координатных осей на расстояние 0, 1 или 2 (без учета направления смещения) с вероятностями, соответственно, p₀=1/4, p₁=1/2, p₂=1/4. Вероятность попадания частицы в данную точку зависит лишь от ее положения в предыдущий момент времени, поэтому рассматриваем движение частицы вдоль оси х (y) как случайное.

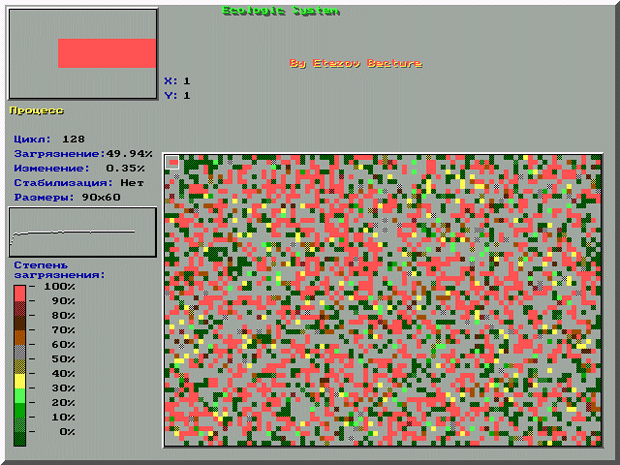
На рис. 1.4 - фрагменты работы программы клеточно-автоматной модели загрязнения клеточной экосреды (размеры клеток увеличены).

Рис. 1.4.

Окно справа - состояние клеточного поля. В верхней таблице показано исходное поле, слабо загрязненное, в нижней таблице показано - после 120 циклов загрязнения, в левом верхнем углу - "Микроскоп", увеличивающий кластер поля, в середине слева - график динамики загрязнения, внизу слева - индикаторы загрязнения.

Модель фрактальная, если она описывает эволюцию моделируемой системы эволюцией фрактальных объектов.

Если физический объект однородный (сплошной), т.е. в нем нет полостей, то можно считать, что плотность не зависит от размера. Например, при увеличении параметра объекта R до 2R масса объекта увеличится в R² раз, если объект- круг и в R³ раз, если объект - шар, т.е. существует связь массы и длины M(R) ~ Rⁿ . Здесь n - размерность пространства. Объект, у которого масса и размер связаны этим соотношением, называется "компактным". Плотность его

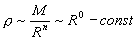
Если объект (система) удовлетворяет соотношению M(R) ~ R^f(n), где f(n) < n, то такой объект называется фрактальным.

Его плотность не будет одинаковой для всех значений R, и она масштабируется так:

Так как f(n) - n < 0, то плотность фрактального объекта уменьшается с увеличением размера, а ρ(R) является количественной мерой разряженности объекта.

Пример. Пример фрактальной модели - множество Кантора. Рассмотрим отрезок [0;1]. Разделим его на 3 части и выбросим средний отрезок. Оставшиеся 2 промежутка опять разделим на три части и выкинем средние промежутки и т.д. Получим множество, называемое множеством Кантора. В пределе получаем несчетное множество изолированных точек (рис. 1.5)

Рис. 1.5. Множество Кантора для 3-х делений

Можно показать, что если n - размерность множества Кантора, то n=ln2/ln3≈0,63, т.е. этот объект (фрактал) еще не состоит только из изолированных точек, хотя уже и не состоит из отрезка.