Математическое моделирование сложных систем

Будем считать, что элемент s есть некоторый объект, обладающий определенными свойствами, внутреннее строение которого для целей исследования не играет роли, например, самолет для моделирования полета – не элемент, а для моделирования работы аэропорта – элемент.

Связь l между элементами есть процесс их взаимодействия, важный для целей исследования.

Система S – совокупность элементов со связями и целью функционирования F.

Сложная система – это система, состоящая из разнотипных элементов с разнотипными связями.

Большая система – это система, состоящая из большого числа однотипных элементов с однотипными связями.

В общем виде систему математически можно представить в виде:

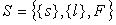
Автоматизированная система SA есть сложная система с определяющей ролью элементов двух типов: технических средств Sт и действий человека SH:

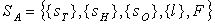
здесь 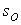- остальные элементы системы.

Структура системыесть разбиение (декомпозиция) системы на элементы или группы элементов с указанием связей между ними, неизменными во время функционирования системы.

Практически все системы рассматриваются функционирующими во времени, поэтому определим их динамические характеристики.

Состояние –это множество характеристик элементов системы, изменяющихся во времени и важных для целей ее функционирования.

Процесс (динамика) –это множество значений состояний системы, изменяющихся во времени.

Цель функционированияесть задача получения желаемого состояния системы. Достижение цели обычно влечет целенаправленное вмешательство в процесс функционирования системы, которое называется управлением.

Задачи исследования систем:

1. Анализ – изучение свойств функционирования системы.

2. Синтез – выбор структуры и параметров по заданным свойствам системы.

Пусть T = [t0, t1] есть временной интервал моделирования системы S (интервал модельного времени).

Построение модели начинается с определения параметров и переменных, определяющих процесс функционирования системы.

Параметры системы 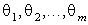- это характеристики системы, остающиеся постоянными на всем интервале T.

Переменные бывают зависимые и независимые.

Независимые переменные есть, как правило, входные воздействия (в том числе управляющие)

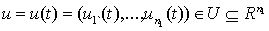
ими могут быть также воздействия внешней среды.

Последовательность изменения x(t) при

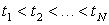
называется фазовой траекторией системы, , где X – пространство состояний или фазовое пространство.

Последовательность изменения y(t) называется выходной траекторией системы.

Зависимые переменные есть выходные характеристики (сигналы)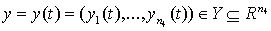

Общая схема математической модели (ММ) функционирования системы может быть представлена в виде:

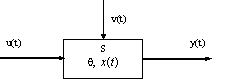
Множество переменных вместе с законами функционирования

называется математической моделью системы.

Если t непрерывно, то модель называется непрерывной, иначе – дискретной:

.

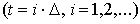Если модель не содержит случайных элементов, то она называется детерминированной, в противном случае – вероятностной.

Если математическое описание модели слишком сложное и частично или полностью неопределенно, то в этом случае используются агрегативные модели.

Сущность агрегативной модели заключается в разбиении системы на конечное число взаимосвязанных частей (подсистем), каждая из которых допускает стандартное математическое описание. Эти подсистемы называются агрегатами.