
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 2. ЛАБОРАТОРНЫЕ РАБОТЫ
№ 1 (+ заочное)
Задание. «Составление схемы структурной связи «Адрон - система «Земля-Луна»» и создание базы физико-химических и др. параметров по разделам: Адрон, Вселенная, Галактика, Черные дыры ,Звезды, Солнечная система, Солнце, планеты».
Исходные данные:
Земля: RЗ =6371 км, MЗ = 5.976 ×1021 т; r =5.517 г/см, ω = 7.29211·10-5с-1;
ωр = 50.25’’/год; H=1/305.51
Галактики: всего 1014; форма: эллиптические, спиральные, линзовидные,
неправильные
Солнце: Излучает энергию 3.9 ×1020 МВт, нормальный карлик, желтый
цвет; Rc = 696265 км; Rядро = 0,3 Rc; Mc = 2 ×1027 т; r = 1,41 г/см3
(ядро 150 т/см3); t0 = 14 млн.°С, Vc = 250 км/c. Состав: водород
70%, гелий 27%, тяжелые эл-ты 3%; время обращения вокруг
центра Галактики 212 млн. лет
Галактика Млечный путь: ~ 200 млрд. Звезд с общей m = 3×1038 т; V = 600 км/c;
D = 100 тыс. свет. лет; Толщина 1 тыс. свет. лет
Звезды: Масса всех звёзд Галактики m = 97% ; 0,1 Mc< MЗвезды<10 Mc; Mc =
2×1027 т
Адрон: Т = 10-44с, D = 10-33 см, r = 1093 г/см3, t0 =1033 0К
Солнечная система: Облако имело массу 2 – 3 Mc; Т = -220°С; Состав: водород,
гелий, азот, кислород, пары воды, метила и углерода;
пылинки: оксид кремния, магния, железа.
Планеты: Тела с m = 1017 – 1026 т; Меркурий, Венера, Земля, Марс,
Пояс астероидов, Юпитер, Сатурн, Уран, Нептун, Плутон,
10-ая планета, Облако астероидов Оорта
Вселенная:
Эра адронная – Взрыв; Т = 10-44 - 10-4 с; D = 10-33 - 109 км, r = 1093 - 1015, t0 =
1033 - 1012; Состав: барионы, мезоны
Эра лептонная - Т=10-4 - 10 с; D = 109 – 3×1012 км, r = 1015 – 1.5×105,
t0 = 1012-1010 0К; Состав: мюоны, электроны, позитроны,
нейтрино, антинейтрино, фотоны
Эра излучения - Т=10с – 106 лет D = 3×1012- 6×1020 км, r = 1.5×105-10-20,
t0 = 1010-3×103 0К; Состав: электроны, протоны, ядра гелия,
фотоны
Эра вещества - Т=106- 2×1010лет D = 6×1020-2×1023км, r =10-20- 3×10-29 г/см3,
t0 = 3×103 0К; Состав: атомы, квазары, черные дыры, галактики,
звёзды, планеты
Примечание: D – поперечные размеры Единицы измерения: 1 а.е. = 149600000 км
r - плотность объекта (тела) 1пк(парсек) = 206265 а.е. = 3.26 св. лет
0К – температура в градусах Кельвина 1 св. год = 9.46·1012 км
m – масса объекта (тела)
M (Mc, MЗ) – масса Солнца, Земли
R (Rc, RЗ) = радиус Солнца, Земли
ω – угловая скорость Земли
ωр – прецессия Земли
V – скорость вращения
Содержание работы:
1. Составить схему структурно-подчиненной связи космических систем во времени, начиная с Большого взрыва и завершая планетами, в частности, Землей.
2. Построить график для эр Вселенной. По оси абсцисс отложить следующие равные доли величины времени: 1 с, 10 с, 1 год, 103 лет, 106 лет, 109 лет, 1012 лет, а по оси ординат – размер эр также равными долями: 1 см, 1 км, 103 км, 106 км, 109 км, 1012 км, 1015 км, 1018 км, 1021 км, 1024 км. Для каждой эры провести границы значений (горизонтально и вертикально) до их пересечения. Каждую эру заштриховать или закрасить.
Дать анализ современного состояния Вселенной. Обосновать, в какой фазе она находится – сжатия, расширения?
№ 2 (+ заочное)
Задание .Геолого-геофизический анализ сейсмических скоростей.
Исходные данные: Скоростной сейсмогеологический разрез по одному из районов Западной Сибири.
| Вариант | |||||||||||||||
| слой1 | |||||||||||||||
| Vp, км/c | 2,58 | 2,6 | 2,62 | 2,64 | 2,66 | 2,68 | 2,7 | 2,72 | 2,74 | 2,76 | 2,78 | 2,8 | 2,82 | 2,84 | 2,86 |
| Vs, км/с | 1,16 | 1,18 | 1,2 | 1,22 | 1,24 | 1,26 | 1,28 | 1,3 | 1,32 | 1,34 | 1,36 | 1,38 | 1,4 | 1,42 | 1,44 |
| h, км | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,1 | 4,2 | 4,3 | 4,4 | ||
| слой2 | |||||||||||||||
| Vp, км/c | 3,68 | 3,7 | 3,72 | 3,74 | 3,76 | 3,78 | 3,8 | 3,82 | 3,84 | 3,86 | 3,88 | 3,9 | 3,92 | 3,94 | 3,96 |
| Vs, км/с | 1,88 | 1,9 | 1,92 | 1,94 | 1,96 | 1,98 | 2,02 | 2,04 | 2,06 | 2,08 | 2,1 | 2,12 | 2,14 | 2,16 | |
| h, км | 9,1 | 9,2 | 9,3 | 9,4 | 9,5 | 9,6 | 9,7 | 9,8 | 9,9 | 10,1 | 10,2 | 10,3 | 10,4 | 10,5 | |
| слой3 | |||||||||||||||
| Vp, км/c | 6,98 | 7,02 | 7,04 | 7,06 | 7,08 | 7,1 | 7,12 | 7,14 | 7,16 | 7,18 | 7,2 | 7,22 | 7,24 | 7,26 | |
| Vs, км/с | 3,98 | 4,02 | 4,04 | 4,06 | 4,08 | 4,1 | 4,12 | 4,14 | 4,16 | 4,18 | 4,2 | 4,22 | 4,24 | 4,26 | |
| h, км | 15,4 | 15,5 | 15,6 | 15,7 | 15,8 | 15,9 | 16,1 | 16,2 | 16,3 | 16,4 | 16,5 | 16,6 | 16,7 | 16,8 | |
| слой4 | |||||||||||||||
| Vp, км/c | 6,08 | 6,1 | 6,12 | 6,14 | 6,16 | 6,18 | 6,2 | 6,22 | 6,24 | 6,26 | 6,28 | 6,3 | 6,32 | 6,34 | 6,36 |
| Vs, км/с | 3,48 | 3,5 | 3,52 | 3,54 | 3,56 | 3,58 | 3,6 | 3,62 | 3,64 | 3,66 | 3,68 | 3,7 | 3,72 | 3,74 | 3,76 |
| h, км | 24,4 | 24,5 | 24,6 | 24,7 | 24,8 | 24,9 | 25,1 | 25,2 | 25,3 | 25,4 | 25,5 | 25,6 | 25,7 | 25,8 | |
| слой5 | |||||||||||||||
| Vp, км/c | 6,28 | 6,3 | 6,32 | 6,34 | 6,36 | 6,38 | 6,4 | 6,42 | 6,44 | 6,46 | 6,48 | 6,5 | 6,52 | 6,54 | 6,56 |
| Vs, км/с | 3,68 | 3,7 | 3,72 | 3,74 | 3,76 | 3,78 | 3,8 | 3,82 | 3,84 | 3,86 | 3,88 | 3,9 | 3,92 | 3,94 | 3,96 |
| h, км | 34,4 | 34,5 | 34,6 | 34,7 | 34,8 | 34,9 | 35,1 | 35,2 | 35,3 | 35,4 | 35,5 | 35,6 | 35,7 | 35,8 | |
| слой6 | |||||||||||||||
| Vp, км/c | 7,28 | 7,3 | 7,32 | 7,34 | 7,36 | 7,38 | 7,4 | 7,42 | 7,44 | 7,46 | 7,48 | 7,5 | 7,52 | 7,54 | 7,56 |
| Vs, км/с | 4,08 | 4,1 | 4,12 | 4,14 | 4,16 | 4,18 | 4,2 | 4,22 | 4,24 | 4,26 | 4,28 | 4,3 | 4,32 | 4,34 | 4,36 |
| h, км | 41,4 | 41,5 | 41,6 | 41,7 | 41,8 | 41,9 | 42,1 | 42,2 | 42,3 | 42,4 | 42,5 | 42,6 | 42,7 | 42,8 |
Содержание работы:
3. Построить график изменения сейсмической скорости как функции глубины:
V = V(h ) (1.1)
4. Найти формулу, аппроксимирующую реальную зависимость скорости от глубины, и оценить ее точность. Формула может иметь вид:
V = Vоexp(-a h) , (1.2)
где Vo - значение скорости в верхней части разреза, h – текущее значение глубины, a - коэффициент, подлежащий определению.
5. Рассчитать вероятные значения плотности (r) для слоев, отличающихся скоростями распространения упругих колебаний:
r = 0,346Vр + 0.646 (1.3)
6. Оценить гравитационную активность каждого из элементов разреза:



где f = 66.7 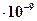 ед. СГС, h1,2 - глубины залегания верхней и нижней поверхностей пластов, L = 100 км – условная горизонтальная мощность пласта.
ед. СГС, h1,2 - глубины залегания верхней и нижней поверхностей пластов, L = 100 км – условная горизонтальная мощность пласта.
5. Рассчитать коэффициенты отражения (Аpp) и прохождения (прозрачности) (Вpp) изучаемой среды: 
|

Bpp= 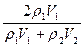
где r1,2 и V1.2 - плотности и скорости распространения продольных сейсмических волн для двух контактирующих слоев разреза.
6.Установить наиболее сильную сейсмическую границу разреза..
7.Сопоставить результаты анализа акустической и гравитационной активности выделяемых геофизических границ разреза.
№ 3
Задание. Приближенная оценка упругих констант изучаемой геологической среды на основании сейсморазведочных материалов.
Исходные данные: сейсмогеологический разрез – данные лабораторной работы №2.
Содержание работы:
1. Рассчитать коэффициенты отношения скоростей распространения продольных) (Vp) и поперечных (Vs) сейсмических волн для всех структурных элементов разреза:
K= Vp/Vs (3.1)
2. Для наиболее крупных структурных элементов геосейсмического разреза оценить следующие параметры:
а) отношение констант Ламе (λ и μ):
(3.2)
|
б) плотность ρ : r = 0,346Vр + 0.646 (формула 1.3 из лаб. раб. 2)
в) модуль сдвига:
μ = VS2·ρ (3.3)
г) постоянную λ = q μ , (3.4)
|
(3.5)
е) модуль Юнга: E = 2Vs2ρ(1+σ) (3.6)
3. Сделать заключение о характере изменения упругих модулей с глубиной и указать элементы разреза, в наибольшей степени подверженные разрывным дислокациям.
№ 4 (+ заочное)
Задание 1. Рассчитать плотность ( 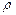 ) внутри Земли для фиксированных глубин по формуле Роша:
) внутри Земли для фиксированных глубин по формуле Роша:
 = 11,35(1-1,07ri2) , где ri = 1 – r//R3 (4.1)
= 11,35(1-1,07ri2) , где ri = 1 – r//R3 (4.1)
| вар-т | ||||||||||||||||||||||||||||||||
| r/, км | ||||||||||||||||||||||||||||||||
по формуле Лежандра:
|
, где ri = 1 – Dhi/R3 (4.2)
если ri- относительное удаление от центра Земли;
Dhi – толщины слоев сейсмической модели земной коры (исх. данные лаб. раб. 2). Даны в км.
| Dh1 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,1 | 4,2 | 4,3 | 4,4 | ||
| Dh2 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 | 6,1 |
| Dh3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 | 6,3 |
| Dh4 | |||||||||||||||
| Dh5 | |||||||||||||||
| Dh6 |
и по формуле Гельмерта:
 = 11,75(1 - 1,04ri2 + 0,275ri4), где ri = 1 – r//R3 (4.3)
= 11,75(1 - 1,04ri2 + 0,275ri4), где ri = 1 – r//R3 (4.3)
| вар-т | ||||||||||||||||||||||||||||||||
| r/, км | ||||||||||||||||||||||||||||||||
R3 – радиус Земли.
Полученные результаты необходимо представить в виде совместных графиков, где по оси абсцисс откладывается расстояние, по оси ординат – рассчитанные значения плотности. Дать анализ расхождению (в %) значений плотности в интервалах пересекающихся (или близких к этому) расстояний r/.
№ 5
Задание. Расчет основных интегральных характеристик Земли: массы Мземли и главных моментов энерции С иА.
Общие положения: А. Моментом энерции данного тела называется отношение момента силы к вызываемому им угловому ускорению. Единица измерения момента энерции в системе СИ: кг×м2. Момент элемента массы Dm, движущегося по окружности радиусом r, равен J=r2×Dm. Для тела с непрерывным распределением массы используется интегральное представление
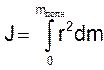
Б. Геоид является поверхностью постоянного геопотенциала U0. В каждой точке Земли полный геопотенциал складывается из потенциала силы тяжести V и члена, зависящего от вращения Земли:
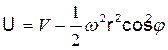
где w - угловая скорость вращения Земли;
r, j - координаты точек на земной поверхности.
На земной поверхности ускорение силы тяжести направлено по нормали к геоиду.
Исходные данные:
RЗемли = 6371 км (средний радиус Земли);
rср = 5.517 г/см3 (средняя плотность Земли);
G = 6.67×10-8 см3/(г×с2) = 6.67×10-11 см3/(г×с2) (гравитационная постоянная);
H = 1/305.51 (константа);
J2 = 1.0827×10-3 (константа);
а = 6378,2 км (экваториальный радиус Земли);
ji = 00, 100, 200, 300, 400, 500, 600, 700, 800;
w = 7.29211×10-5 с-1 (угловая скорость Земли).
Содержание работы:
7. Вычислить полярный момент инерции Земли:

8. Вычислить экваториальный момент инерции Земли А из выражения:

9. Вычислить значения поверхности геоида:

где 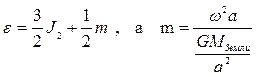
4. Вычертить поверхность геоида для 4-х четвертей, вынести на его поверхность условные материки и указать направления ускорения силы тяжести для углов j = 00, 300, 600, 900. Дать пояснения. Отметить (жирными линиями) главные оси моментов инерции С и А.
№ 6
Çàäàíèå. Прямая и обратная задачи для однородного шара в гравиметрии.
Исходные данные: Однородный шар свинцовых руд с плотностью s, общей массой М, радиусомRи глубиной залеганияh, равной расстоянию от дневной поверхности до центра шара.
Содержание работы:
1.
 |
Решить прямую задачу - вычислить значения вертикальной составляющей потенциала притяжения Vz(в мГл)на дневной поверхности от однородного шара в точках наблюденияPiвдоль линии, проходящей через его эпицентр:
гдеri - расстояние от эпицентра до точки вычисленияPiвдоль выбранной линии;текущиезначения riдля вычисления Vz(ri): 0, 25, 50, 75, 100, 125, 150…….. 400, 5000 (в метрах).
Mш– масса шара в граммах, вычисляется по формуле:
Mш= 4pR3sизб/3; (6.2)
R, hци ri– расстояния в см;
G= 66.7õ10-9, см3/(г·с2).
sсв- плотность свинцовых руд,г/см3; sизб=(sсв– 2.7), г/см3;
2. Построить график Vz(ri).
3.
 |
Вычислить значения вертикальной составляющей потенциала притяженияVznпри тех же условиях, что и в п.1, но по заданному значению амплитуды Vzn в эпицентреVzn(0) = 1.5Vz(0) = Emax:
 |
4. Построить график Vzn(ri).
5. Решить обратную задачу для Vzn(ri): 
à) вычислить значение глубины расположения центра шара по формуле
hn= 1.305r1/2, (6.4)
гдеr1/2– расстояние от эпицентра до точки P, для которой потенциал притяжения равен Emax/2;Emax/2=(Е(0)+Е(400))/2;
 |
á) вычислить радиус шара по формуле
знаяEmaxиhn.ЗдесьEmaxв мГл, hn– вм, тогдаRn– вм. Теперь находим: 
5. Выполнить анализ соотношений hn/h,snnизб/sизби Rn/R, исходя из заданного условия Vzn(0)/Vz(0)=1.5. Объяснить, способны ли вновь рассчитанные параметры пласта создать аномалию, в 1.5 раза превышающую исходную аномалию. Сделать расчет по формуле (6.1).
№ 7 (+ заочное)
Задание. Расчет прецессии Земли wр, обусловленной приливными влияниями Луны wрL и Солнца wрC.
Исходные данные:
G – гравитационная постоянная, 6.67×10-11, м3/кг×с2;
r- средняя плотность Земли, 5.517 г/см3;
kC – отношение массы Солнца к массе Земли и равно 3.329×105;
kL - отношение массы Луны к массе Земли и равно 0.0123.
W - угловая скорость Земли, 7.29212×10-5 с-1; - согласно варианту
RC – радиус орбиты Земли относительно Солнца, 1.496×108;
RL – радиус орбиты Луны относительно Земли, 384.4×103;
(С-А)/С – динамическое сжатие Земли, 3.2732×10-3;
q - угол наклона подвижной оси Земли относительно вертикальной оси, 23.50.
P.S. Дуга, равная радиусу, имеет 57017¢44¢¢.8 (=) радиан; 1¢¢ = 0.484814×10-5.
Содержание работы:
1. Вычислить величину прецессии Земли в год (wр, ¢¢/год), обусловленной приливными влияниями Луны и Солнца:
 |
wр = wрL+ wрC , где
и
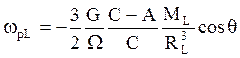 |
Указания: вычислить массы Луны (ML) и Солнца (MC) через массу Земли (MZ) и отношения масс Луны и Солнца к массе Земли.
2. Сделать заключение о степени влияния каждого объекта (Луны и Солнца) на прецессию Земли, исходя из отношений:
а = wр/wрL и b = wр/wрС
№ 8 (+ заочное)
Задание. Построить поле времен прямой волны и годограф отраженной волны в случае источника, расположенного внутри упругой земной среды.
Исходные данные: Источник сейсмических колебаний расположен под земной поверхностью в точке с координатами Р(0,0,-z), где z = -50 м. Приемники расположены на линии профиля в точках:;
xi(-500, 0, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 5500, 6000, 6500, 7000, 7500), м;
yi(-500, 0, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 5500, 6000, 6500, 7000, 7500), м.
Глубина до отражающей вогнутой границы с радиусом R=-2500 м под точками наблюдения составляет:
hi(800, 900, 1300, 1500, 1800, 1200, 1000, 850, 650, 600, 550, 500, 450, 400, 350), м.
Скорость распространения прямой и отраженной волны Vp(l) равна (для вариантов):
(1)3000, (2)3100, (3)3200, (4)3300, (5)3400, (6)3500, (7)3600, (8)3700, (9)3800, (10)3900, (11)4000, (12)4100, (13)4200, (14)4300, (15)4400), м/с.
Содержание работы:
1.
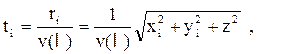 |
Рассчитать поле времен (изохроны) для сейсмических колебаний от источника, расположенного согласно данным (z = -50 м), по формуле:
Для построения поля времен необходимо вычислить радиус r’, откладываемый по горизонтали плоскости (земной поверхности) от эпицентра источника колебаний О’:
 |
2. Построить изохроны (поле времен) в аксонометрии, зная что t(i) = f(xi,yi,z) = f(r’).
3.
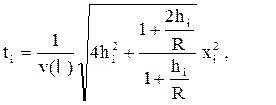 |
Вычислить годограф сейсмической волны, отраженной от криволинейной вогнутой границы, заданной данными xi, yi, hi и R при определенной скорости Vp(l) (где l – вариант) по формуле (источник волны находится непосредственно под поверхностью земли):
4. Построить график годографа ti.
Выполнить анализ причины образования у годографа “петли” и показать это на схематическом рисунке.
№ 9
Задание. Расчет температуры земной и океанической коры Тi на различных глубинах zi относительно уровня моря.
Исходные данные: Заданы а) общие исходные параметры модели:
- тип теплопроводности – решеточный;
- температура поверхности Земли Т0 = 100С;
- температура воздуха Тп = 180С;
- расчетные глубины, км: 20, 30, 40, 50.
б) для земной коры:
- тепловой поток Qз.к. = 0.58х10-6 кал/см2сек;
- генерация тепла на 1 см3 Рз.к. = 1.4х10-13 кал/см3сек;
- коэффициент теплопроводности cземн.кора = (в соответствии с вариантом), (кал/( см·с·К));
в) для океанической коры:
- тепловой поток Qз.к. = 0.75х10-6 кал/см2сек;
- генерация тепла на 1 см3 Рз.к. = 1.15х10-13 кал/см3сек;
- коэффициент теплопроводности cокеан = (в соответствии с вариантом), (кал/( см·с·К));
cокеан: 0.0252(1), 0.0253(2), 0.0254(3), 0.0255(4), 0.0256(5), 0.0257(6), 0.0258(7), 0.0259(8), 0.026(9), 0.0261(10), 0.0262(11), 0.0263(12), 0.0264(13), 0.0265(14), 0.0266(15)
cземн.кора: 0.0152(1), 0.0153(2), 0.0154(3), 0.0155(4), 0.0156(5), 0.0157(6), 0.0158(7), 0.0159(8), 0.016(9), 0.0161(10), 0.0162(11), 0.0163(12), 0.0164(13), 0.0165(14), 0.0166(15)
В скобках приведены номера вариантов.
Содержание работы:
10.
 |
вычислить величины температуры Тi на различных глубинах zi для земной и океанической коры по теоретической формуле В.А. Магницкого:
11. Построить совмещенные графики изменения температуры Тi как функции глубины от zi для земной и океанической коры.
12. Вычислить величины температуры Тi на различных глубинах zi для земной и океанической коры по эмпирическим формулам В.А. Магницкого соответственно:
13.
 |
Построить эмпирические графики Тi на предыдущих Тi.
Сделать заключение о применимости тех или иных формул для расчета температур на основе решеточной теплопроводности, если исходить из условия, что на глубине порядка 100 км температура должна быть близка к температуре плавления базальтов 12000С, но не превышать 20000С.
В процесс проработки теоретического материала для лучшего усвоения курса студент заочного обучения должен выполнить контрольную работу. Вариант задания контрольной работы совпадает с последней цифрой зачетной книжки.
Дата добавления: 2015-01-29; просмотров: 1141; Мы поможем в написании вашей работы!; Нарушение авторских прав |



