
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Грамматики типа 3
Грамматики типа 3 называют автоматными грамматиками (А - грамматиками). Правила вывода в таких грамматиках имеют вид:
<A>  a или <A>
a или <A>  a<B> или <A>
a<B> или <A>  <B>a,
<B>a,
где a  Vт, <A>, <B>
Vт, <A>, <B>  VА, причем грамматика может иметь только правила вида <A>
VА, причем грамматика может иметь только правила вида <A>  a<B> - правосторонние правила, либо только вида <A>
a<B> - правосторонние правила, либо только вида <A>  <B>a - левосторонние правила. Примерами автоматных грамматик могут служить правосторонняя грамматика Г1. 6 и левосторонняя грамматика Г1. 7.
<B>a - левосторонние правила. Примерами автоматных грамматик могут служить правосторонняя грамматика Г1. 6 и левосторонняя грамматика Г1. 7.
Г1. 6
Vт = {a, b}, VА = {<I>, <A>},
R = { <I>  a<I>,
a<I>,
<I>  a<A>,
a<A>,
<A>  b<A>,
b<A>,
<A>  b<Z>,
b<Z>,
<Z>  $ }
$ }
Г1. 7
Vт = {a, b}, VА = {<I>, <A>},
R = { <I>  <A>b,
<A>b,
<A>  <A>b,
<A>b,
<A>  <Z>a,
<Z>a,
<Z>  <Z>a,
<Z>a,
<Z>  $ }
$ }
Эти грамматики являются эквивалентными и порождают язык
L(Г7) = {a...ab...b | n,m > 0}
Между множествами языков различных типов существует отношение включения:
{ L типа 3 }  { L типа 2 }
{ L типа 2 }  { L типа 1 }
{ L типа 1 }  { L типа 0 }
{ L типа 0 }
Доказано, что существуют языки типа 0, не являющиеся языками типа 1, языки типа 2, не являющиеся языками типа 1, и языки типа 3, не являющиея языками типа 2.
7. Запуск программы LEX. Задание классов символов. Задание произвольных символов. Задание вариантов. Какое имя по умолчанию получает файл исходного кода лексического анализатора, который формирует генератор LEX. Для запуска программы LEX необходимо ввести в терминале следующие команды: lex <name>.l, далее gcc lex.yy.c и ./a.out, где <name> - имя программы LEX. Для обозначения класса символов применяются метасимволы, образующие пару квадратных скобок []. Внутри квадратных скобок должно быть задано множество символов, любой из которых может присутствовать в данной позиции входной строки. При этом следует учитывать, что внутри квадратных скобок класса символов большая часть метасимволов игнорируется. Специальными являются только три символа: обратная дробная черта (\), дефис (-) и циркумфлекс (^). Причем метасимвол (^) имеет различный специальный смысл внутри класс символов и вне его границ. Для обозначения вариантов в регулярных выражениях используется метасимвол вертикальной черты |, который имеет аналогичный смысл логического оператора ИЛИ, например, в языках программирования C, C++, C# и Java. GRAY|GREY
Это регулярное выражение обеспечивает выбор любого из двух допустимых альтернативных вариантов входного слова: GRAY или GREY.
имя по умолчанию для файла исходного кода лексического анализатора, который формирует генератор LEX - lex.yy.c
8. Грамматика G задана следующими правилами: …. приведите грамматику к нормальной форме Хомского.
Нормальная форма Хомского — свойство формальной грамматики, если все её продукции имеют вид:
  или или
 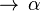 или или
  ,
где ,
где  , ,  и и  — нетерминалы, — нетерминалы,  — терминальный символ (представляющий постоянное значение), — терминальный символ (представляющий постоянное значение),  — начальный символ, и — начальный символ, и  — пустая строка. Также ни — пустая строка. Также ни  , ни , ни  не может быть начальным символом.
Каждая грамматика в нормальной форме Хомского является контекстно-свободной, и наоборот, каждая контекстно-свободная грамматика может быть эффективно преобразована в эквивалентную грамматику в нормальной форме Хомского. не может быть начальным символом.
Каждая грамматика в нормальной форме Хомского является контекстно-свободной, и наоборот, каждая контекстно-свободная грамматика может быть эффективно преобразована в эквивалентную грамматику в нормальной форме Хомского.
|
Рассмотрим контекстно-свободную грамматику 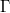 . Для приведения ее к нормальной форме Хомского необходимо выполнить пять шагов. На каждом шаге мы строим новую . Для приведения ее к нормальной форме Хомского необходимо выполнить пять шагов. На каждом шаге мы строим новую  , которая допускает тот же язык, что и , которая допускает тот же язык, что и 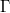 .
1. Уберём длинные правила.
Воспользуемся алгоритмом удаления длинных правил из грамматики. Получим грамматику .
1. Уберём длинные правила.
Воспользуемся алгоритмом удаления длинных правил из грамматики. Получим грамматику  , эквивалентную исходной, содержащую правила длины 0, 1 и 2.
Пусть , эквивалентную исходной, содержащую правила длины 0, 1 и 2.
Пусть 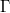 — контекстно-свободная грамматика. Правило — контекстно-свободная грамматика. Правило  называется длинным если называется длинным если  .
Пример работы
Покажем, как описанный алгоритм будет работать на следующей грамматике: .
Пример работы
Покажем, как описанный алгоритм будет работать на следующей грамматике:


 .
Для правила .
Для правила  вводим вводим  новых нетерминала новых нетерминала 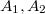 и и  новых правила: новых правила:


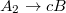 .
Для правила .
Для правила  вводим вводим  новый нетерминал новый нетерминал  и и  новых правила: новых правила:

 .
В итоге полученная грамматика .
В итоге полученная грамматика 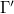 будет иметь вид: будет иметь вид:



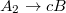

 .
2. Удаление .
2. Удаление  -правил.
Правила вида -правил.
Правила вида  называются называются  -правилами ( -правилами (  rule).
Воспользуемся алгоритмом удаления rule).
Воспользуемся алгоритмом удаления  -правил из грамматики. Получим грамматику -правил из грамматики. Получим грамматику 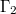 , эквивалентную исходной, но в которой нет , эквивалентную исходной, но в которой нет  -правил.
Пример
Рассмотрим грамматику: -правил.
Пример
Рассмотрим грамматику: 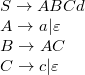 , в которой , в которой 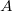 , , 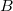 и и  являются являются  -порождающими нетерминалами.
1. Переберём для каждого правила все возможные сочетания ε-порождающих нетерминалов и добавим новые правила:
§ -порождающими нетерминалами.
1. Переберём для каждого правила все возможные сочетания ε-порождающих нетерминалов и добавим новые правила:
§  для для  §
§  для для  2. Удалим праила
2. Удалим праила  и и  В результате мы получим новую грамматику без
В результате мы получим новую грамматику без  -правил: -правил:  3. Удаление цепных правил.
Цепное правило (unit rule) — правило вида
3. Удаление цепных правил.
Цепное правило (unit rule) — правило вида 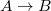 , где , где 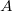 и и 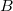 — нетерминалы.
Воспользуемся алгоритмом удаления цепных правил из грамматики. Алгоритм работает таким образом, что новые — нетерминалы.
Воспользуемся алгоритмом удаления цепных правил из грамматики. Алгоритм работает таким образом, что новые  -правила не образуются. Получим грамматику -правила не образуются. Получим грамматику  , эквивалентную , эквивалентную 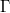 .
Пример
Рассмотрим грамматику: .
Пример
Рассмотрим грамматику: 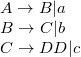 , в которой есть два цепных правила , в которой есть два цепных правила 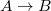 и и 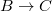 .
1. Для каждого нетерминала создадим цепную пару. Теперь множество цепных пар будет состоять из .
1. Для каждого нетерминала создадим цепную пару. Теперь множество цепных пар будет состоять из 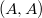 , ,  , , 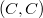 и и 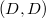 .
2. Рассмотрим цепное правило .
2. Рассмотрим цепное правило 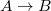 . Так как существует цепная пара . Так как существует цепная пара 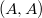 , второй элемент которой совпадает с левым нетерминалом из правила, добавим в множество пару , второй элемент которой совпадает с левым нетерминалом из правила, добавим в множество пару 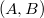 , у которой первый элемент такой же как у найденной, а второй равен правому нетерминалу из текущего правила.
3. Повторим второй пункт для правила , у которой первый элемент такой же как у найденной, а второй равен правому нетерминалу из текущего правила.
3. Повторим второй пункт для правила 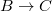 и пары и пары  . Теперь множество цепных пар будет состоять из . Теперь множество цепных пар будет состоять из 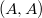 , ,  , , 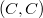 , , 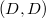 , , 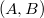 и и 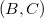 .
4. Повторим второй пункт для правила .
4. Повторим второй пункт для правила 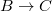 и пары и пары 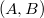 , и получим множество , и получим множество  .
5. Для каждой пары добавим в .
5. Для каждой пары добавим в 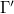 новые правила:
§ новые правила:
§  для для 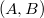 §
§ 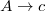 и и 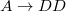 для для 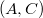 §
§  и и  для для 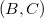 § Оставшиеся цепные пары новых правил не добавят.
4. Удалим бесполезные символы.
Нетерминал
§ Оставшиеся цепные пары новых правил не добавят.
4. Удалим бесполезные символы.
Нетерминал 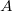 называется порождающим (generating), если из него может быть выведена конечная терминальная цепочка. Иначе он называется непорождающим.
Воспользуемся алгоритмом удаления бесполезных символов из грамматики. Так как называется порождающим (generating), если из него может быть выведена конечная терминальная цепочка. Иначе он называется непорождающим.
Воспользуемся алгоритмом удаления бесполезных символов из грамматики. Так как  эквивалентна эквивалентна 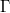 , то бесполезные символы не могли перестать быть бесполезными. Более того, мы только удаляем правила, новые , то бесполезные символы не могли перестать быть бесполезными. Более того, мы только удаляем правила, новые  -правила и цепные правила не могли появиться.
Пример
Рассмотрим грамматику: -правила и цепные правила не могли появиться.
Пример
Рассмотрим грамматику:  1. Возьмём множество, состоящее из единственного элемента:
1. Возьмём множество, состоящее из единственного элемента:  .
2. Из .
2. Из  достижимы нетерминалы достижимы нетерминалы 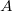 , , 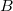 , ,  и и  . Добавим их в множество и получим . Добавим их в множество и получим  .
3. Множество изменилось. Переберём заново правила из грамматики. Из .
3. Множество изменилось. Переберём заново правила из грамматики. Из 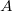 можно вывести можно вывести  и и  , добавим их в множество.
4. Снова переберём правила. Из , добавим их в множество.
4. Снова переберём правила. Из  можно вывести только терминал, а можно вывести только терминал, а 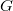 нету в множестве.
5. После последнего обхода правил грамматики множество не изменилось, значит мы нашли все достижимые нетерминалы: нету в множестве.
5. После последнего обхода правил грамматики множество не изменилось, значит мы нашли все достижимые нетерминалы:  .
6. Теперь удалим правило .
6. Теперь удалим правило  , так как оно содержит в левой части нетерминал, которого нет в полученном множестве.
5. Уберём ситуации, когда в правиле встречаются несколько терминалов.
Для всех правил вида , так как оно содержит в левой части нетерминал, которого нет в полученном множестве.
5. Уберём ситуации, когда в правиле встречаются несколько терминалов.
Для всех правил вида  (где (где  — терминал или нетерминал) заменим все терминалы — терминал или нетерминал) заменим все терминалы  на новые нетерминалы на новые нетерминалы  и добавим правила и добавим правила  . Теперь правила содержат либо одиночный терминал, либо строку из двух нетерминалов.
Таким образом, мы получили грамматику в нормальной форме Хомского, которая допускает тот же язык, что и . Теперь правила содержат либо одиночный терминал, либо строку из двух нетерминалов.
Таким образом, мы получили грамматику в нормальной форме Хомского, которая допускает тот же язык, что и 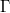 . .
|
Пример
Преобразовать в нормальную форму Хомского КС-грамматики 
1. 
1. удаляем е правила
2. удаляем цепные правила
3. удаляем бесполезные символы
1.
S->AB
A->SA|BB|bB
B->b|aA|e
удаляем е правила
S->A|AB
A->SA|BB|B|bB|b
B->b|aA
удаляем цепные
(S,S)&S->A (S,A)
(S,A)&A->B (S,B)
(S,S) S->AB
(S,A) S->SA|BB|bB|b
(S,B) S->b|aA
S->AB|SA|BB|bB|b|aA
A->SA|BB|bB|b
B->a|aA
Удаляем бесполезные
9. Контекстно-свободные и контекстно-зависимые грамматики. См. вопрос 6 (классификация грамматик Хомского).
10. Построить конечный автомат для следующего регулярного выражения…. предварительно его преобразовав.
Пример построения конечного автомата:
1.Формулировка задания: d|a2(ab)*c
2.Диаграмма переходов конечного автомата:

Примечание:

| – обозначение начального состояния |

| – обозначение конечного состояния |

| – обозначение перехода изсостояния q1 вcсостояние q2 илипо a илипо b |
3.Построенный автомат является недетерминированным, потому что есть е-переходы. Детерминируем конечный автомат.

4.Для полученного конечного автомата построим таблицу состояний.
| a | b | c | d | |
| q0 | q1 | q2 | ||
| q1 | q3 | |||
| q2 | ||||
| q3 | q4 | q2 | ||
| q4 | q5 | |||
| q5 | q4 | q2 |
5.Конечный автомат является неминимизированным. Минимизируем .
Вводим дополнительное состояниеq6

Строим дерево разбора.
Алгоритм минимизации.
1. Пусть множество П(0,1,2,3,4,5,6) – множество всех состояний. Разобьем его на два подмножества согласно условию с состояниями (0,1,2,3,4,6) и (5).
2. Первое подмножество разбиваем еще на 2 с состояниями (0,1,3,6) и (2,4), потому что для всех входных символов переход по входному символу в состояние из одной и той же группы.
3. Первое подмножество делим на 2 с состояниями (0,1,6) и (3).
4. Перовое подмножество делим на 2 с состояниями (0,6) и (1).
5. Первое подмножество после предыдущего деления делим на 2 с состояниями (0) и (6).
В результате получили, что из состояний 2 и 4 можно оставить только одно, например 2. Количество состояний конечного автомата уменьшилось на одно.

Из полученного дерева видим, что состояния q2 иq4можно объединить в одно состояние q3.

Получили детерминированный и минимизированный конечный автомат.
11. Порождающие грамматики. Основные определения и аксиомы. Примеры. Порождающая грамматика задается упорядоченной четверкой  , в которой
, в которой 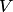 — алфавит, называемый терминальным алфавитом;
— алфавит, называемый терминальным алфавитом;  — алфавит, называемый нетерминальным алфавитом, причем пересечение
— алфавит, называемый нетерминальным алфавитом, причем пересечение 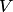 и
и  пусто;
пусто;  — выделенный символ нетерминального алфавита, называемый аксиомой;
— выделенный символ нетерминального алфавита, называемый аксиомой;  — конечное множество правил вывода, или продукций. Каждое правило вывода является упорядоченной парой
— конечное множество правил вывода, или продукций. Каждое правило вывода является упорядоченной парой  цепочек в алфавите
цепочек в алфавите  , причем цепочка
, причем цепочка  должна содержать вхождение хотя бы одного символа нетерминального алфавита; цепочку
должна содержать вхождение хотя бы одного символа нетерминального алфавита; цепочку  называют левой, цепочку
называют левой, цепочку  — правой частью правила вывода.
— правой частью правила вывода.
Правило вывода принято записывать в таком виде:  , разделяя левую и правую части "стрелкой", которая рассматривается как "метасимвол" и не принадлежит ни одному из алфавитов грамматики. Буквы терминального алфавита грамматики называют терминальными символами (или просто терминалами); буквы нетерминального алфавита называют нетерминальными символами (или нетерминалами). Любую цепочку в терминальном (нетерминальном) алфавите называют терминальной (нетерминальной) цепочкой. Алфавит
, разделяя левую и правую части "стрелкой", которая рассматривается как "метасимвол" и не принадлежит ни одному из алфавитов грамматики. Буквы терминального алфавита грамматики называют терминальными символами (или просто терминалами); буквы нетерминального алфавита называют нетерминальными символами (или нетерминалами). Любую цепочку в терминальном (нетерминальном) алфавите называют терминальной (нетерминальной) цепочкой. Алфавит  называют объединенным алфавитом грамматики
называют объединенным алфавитом грамматики  .
.
Пример 7.3. Четверка

задает грамматику с терминальным алфавитом  , с нетерминальным алфавитом
, с нетерминальным алфавитом  , с аксиомой
, с аксиомой  и множеством правил вывода
и множеством правил вывода  , элементы которого перечислены в фигурных скобках после аксиомы. Обычно ради наглядности правила вывода грамматики выписывают отдельно:
, элементы которого перечислены в фигурных скобках после аксиомы. Обычно ради наглядности правила вывода грамматики выписывают отдельно: 
12. Магазинный автомат (автомат с магазинной памятью). Определение. Магазинный автомат М определяется следующей совокупностью семи объектов:
M = {P , S , sо , f , F , H , hо }, где
P - входной алфавит,
S - алфавит состояний,
sо - начальное состояние,
sо  S ,
S ,
F - множество конечных состояний, F является подмножеством S,
H - алфавит магазинных символов, записываемых на вспомогательную ленту,
hо - маркер дна, он всегда записывается на дно магазина, hо  H,
H,
f - функция переходов
f : {P  { ε }} x S x H
{ ε }} x S x H  S x H*,
S x H*,
если М - автомат детерминированный, и
f:{P  { ε }} x S x H
{ ε }} x S x H  M( S x H*) ,
M( S x H*) ,
если М - автомат недетерминированный.
Функция f отображает тройки ( pi, sj, hk) в пары ( sr, υ ), где υ  H* и hk - символ в вершине магазина, для детерминированного автомата или в множество пар для недетерминированного автомата.
H* и hk - символ в вершине магазина, для детерминированного автомата или в множество пар для недетерминированного автомата.
Эта функция описывает изменение состояния магазинного автомата, происходящее при чтении символа с входной ленты и премещении входной головки.
В дальнейшем при построении магазинных автоматов потребуются две разновидности функций переходов, изменяющих состояние автомата без перемещения входной головки:
1) функция переходов с пустым символом в качестве входного символа:
f0(s, ε, h) = (s', β),
которая, независимо от того какой символ находится под читаюшей гловкой входной ленты, предписывает прочитать символ h из вершины магазина, изменить состояние автомата на s' и записать цепочку β в магазин.
2) функция переходов с определенным входным символом:
f*(s, a, h) = (s', β),
которая предписывает изменение состояния и запись цепочки в магазин при условии, что символ a читается входной головкой, а в вершине магазина находится символ h.

ПРИМЕР ПОСТРОЕНИЯ МП АВТОМАТА:
Пусть дана грамматика
G = ({a,b,c},{S},S,P),
множество правил вывода Р которой есть
S ® aSbS | aS | c.
Тогда эквивалентный ей МП-автомат задается следующей системой команд:
qλS ®qaSbS | qaS | qc,
qaa ® qλ,
qbb ® qλ,
qcc ® qλ
(мы использовали сокращенную запись нескольких команд с одинаковыми левыми частями по аналогии с тем, как мы это делаем при записи множества правил вывода грамматики).
В системе команд МП-автомата, который строится по заданной КС-грамматике так, как это описано выше, мы видим два „сорта" команд: 1) команды, „моделирующие" применение правил, исходной грамматики (в данном примере это команды первой строки); при выполнении каждой такой команды МП-автомат делает λ-такт, т.е. не продвигает головку по входной ленте; 2) команды „сравнения", согласно которым МП-автомат должен убирать верхний символ магазина всякий раз, когда он совпадает с обозреваемым символом на ленте.
Тогда, читая входную цепочку, такой МП-автомат „моделирует" левый вывод этой цепочки в исходной грамматике, применяя каждый раз, когда верхним символом магазина оказывается нетерминал, команду „первого сорта" и всякий раз, когда верхним символом магазина оказывается терминал исходной грамматики, „команду сравнения".
Прочитаем цепочку aacbc:

Нетрудно видеть, что этот вывод „моделирует" левый вывод в грамматике:

т.е. МП-автомат, строя допускающую последовательность конфигураций для входной цепочки, на каждом шаге, когда верхний символ магазина не совпадает с очередным символом входной цепочки, должен „угадать" применяемое правило (выбрать в данном примере одну из трех первых команд). Неправильный выбор приведет к тупику, например:

13. Среда выполнения YACC. Какие разновидности конфликтов свойственны неоднозначным грамматикам для принятого в YACC метода грамматического разбора. Среда выполнения YACC: при подаче на вход yacc спецификации, на выходе получается файл с программой на языке С, чаще всего называемый y.tab.c. В нем содержится функция, возвращающая целое, по имени yyparse(). Для получения входных лексем эта функция вызывает функцию лексического анализатора yyerror(). Далее, либо будет обнаружена ошибка и в этом случае (если не задано действий по обработке ошибок) yyparse() вернет 1, либо лексический анализатор вернет конечный маркер и распознаватель завершит обработку возвратом 0. Для получения работающей прёограммы пользователь должен снабдить распознаватель некоторой средой выполнения. Например, как у любой программы на С должна существовать функция main, всегда вызывающая yyparse(). Далее, для печати сообщений об ошибках должна вызываться функция yyerror().
Эти функции в той или иной форме должны задаваться пользователями. Для облегчения этой задачи существует библиотека, содержащая версии по умолчанию для функций main() и yyerror(). Имя библиотеки зависит от системы, во многих системах она задается флагом -ly компоновщика.
Разновидности конфликтов – см. вопрос 3 (неоднозначности и конфликты).
Дата добавления: 2015-01-29; просмотров: 760; Мы поможем в написании вашей работы!; Нарушение авторских прав |