У точках середовища, де

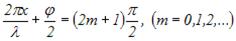
. Ці точки називаються вузлами стоячої хвилі. Точки середовища, що знаходяться у вузлах, не коливаються.

Виберемо початок відліку 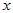так, щоб 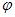дорівнювало нулю. Тоді координати пучностей

,

а вузлів

.

Відстань між двома сусідніми пучностями отримаємо, якщо знайдемо різницю двох значень для двох послідовних значень :

тобто відстань між сусідніми пучностями дорівнює половині довжини тих хвиль, в результаті інтерференції яких утворюється дана стояча хвиля.

Відстані вузла від найближчої пучності дорівнює:

.

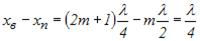(Пучности – точки, в которых амплитуда стоячей волны максимальна :

- координата пучности

Узлы стоячей волны – точки, в которых амплитуда стоячей волны равна нулю :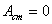

- координата узлов

Границы максимальных смещений точек среды в зависимости от их координат изображены на рисунке. Здесь же отмечены коор­динаты х₀,, х₁, х₂ , ... узлов и координаты х'₀, х'₁, х'₂ ... пуч­ностей стоячей волны.)

Отже, в стоячій хвилі є ряд нерухомих вузлових точок, які розміщені на відстані півхвилі одна від одної. Частинки між вузлами коливаються з різними амплітудами, від нуля у вузлі до подвійної амплітуди у пучності. Всі частинки одночасно проходять через положення рівноваги і одночасно досягають максимальних відхилень, отже, коливаються в однакових фазах. В суміжному інтервалі між вузлами характер коливань такий самий, але фаза протилежна.

У стоячій хвилі енергія не перено-ситься – повна енергія коливань кожного елемента об’єму середовища, обмеженого сусіднім вузлом і пучністю, не залежить від часу. Вона лише переходить з кінетичної енергії в потенціальну енергію пружно деформованого середовища і навпаки. Від-сутність перенесення енергії стоячою хви- лею є результатом того, що падаюча і від- бита хвилі, які утворюють цю стоячу хви- лю, переносять енергію в рівних кількос- тях і в протилежних напрямках.

3. Світло, в якому напрямки коливань якимсь чином впорядковані, називається поляризованим.
Поляризація світла – це така його властивість, яка характеризується просторово-часовою впорядкованістю орієнтації векторів напруженостей електричного та магнітного полів. Під терміном “поляризація світла” розуміють також процес отримання поляризованого світла.

Подвійне заломлення променів має місце в природних анізотропних середовищах. Проте існують різні способи отримання штучної оптичної анізотропії, тобто надання її від природи ізотропним речовинам.

Оптично ізотропні речовини стають оптично анізотропними під дією:

1)одностороннього стискання або розтягу (кристали кубічної системи, скло, .); 2) електричного поля (ефект Керра, рідини, аморфні тіла, гази); 3) магнітного поля (рідини, скло, колоїди). У перелічених випадках речовина набуває властивостей одноосного кристала, оптична вісь якого збігається з напрямком деформації, або напрямками дії електричного чи магнітного полів.

Мірою оптичної анізотропії є різниця показників заломлення звичайного і незвичайного променів у напрямку, перпендикулярному до оптичної осі:

при дії деформації – (n0 – ne) = k1σ;

при дії електричного поля - (n0 – ne) = k2E2;

при дії магнітного поля - (n0 – ne) = k3H2., (36)

де k1, k2, k3 – сталі, які характеризують речовину, σ – нормальна напруга, Е і Н – відповідно напруженості електричного і магнітного полів.

На рис.23 зображена принципова схема для спостереження ефекта Керра у рідинах ( установки для вивчення розглянутих явищ подібні ).

Комірка Керра (кювета з рідиною, наприклад нітробензолом), в яку занурено обкладки плоского конденсатора, розміщена між схрещеними (α = 900 ) поляризатором Р та аналізатором А. При відсутності електричного поля світло не проходить крізь систему. Під дією однорідного електричного поля рідина поляризується і набирає властивостей одноосного двозаломлюючого кристала. При зміні різниці потенціалів між електродами змінюється ступінь анізотропії речовини, а звідси – і інтенсивність світла, яке проходить крізь аналізатор. На шляху l між звичайним і незвичайним променями виникає різниця ходу Δ = l (n0 - ne) = k2lE2 ( з урахуванням виразу (36))

і відповідно різниця фаз δ = 2πΔ/λ = 2πBlE 2, де B = k2/λ - стала Керра.

Ефект Керра - оптична анізотропія речовини під дією електричного поля – пояснюється різною поляризацією молекул рідини в різних напрямках. Це явище практично безінерційне, тобто перехід речовини з ізотропного стану в анізотропний при вмикання поля (і навпаки) не перевищує 10-10с. Тому комірка Керра широко використовується як швидкодіючий світловий затвор у швидкоплинних процесах (записування та відтворення звуку, швидкісна фото- і кінозйомка, визначення швидкості поширення світла і т.п.) .

Штучна оптична анізотропія під дією механічної деформації дозволяє вивчати напруги, що виникають в прозорих тілах. В даному випадку про ступінь деформації окремих ділянок (наприклад, залишкових внутрішніх напруг у склі при його загартуванні) роблять висновок по розподілу в об’єкті забарвлення. Оптичний метод вивчення на прозорих моделях розподілу внутрішніх напруг у різних непрозорих частинах машин і споруд широко застосовують у сучасній техніці. Для цього використовують моделі, виготовлені з прозорих матеріалів, а потім роблять відповідний перерахунок на конструкцію, яка проектується.

Всі прозорі кристали (крім кристалів кубічної системи, які оптично ізотропні) здатні до подвійного заломлення променів, тобто промінь світла, що падає на поверхню кристала , роздвоюється в ньому на два заломлені промені, які в загальному випадку мають різні напрями. Це явище, вперше виявлене датським вченим Е.Бартоліном (1625-1698р.р.) для ісландського шпату (різновидність кальциту CaCO3), пояснюється особливостями розповсюдження світла в анізотропних середовищах.
Якщо на товстий кристал ісландського шпату падає вузький пучок світла, то з кристалу вийдуть два просторово розділені промені, паралельні один одному і падаючому променю. І в тому випадку, коли первинний пучок падає на кристал нормально, заломлений пучок розподіляється на два, причому один з них є продовженням первинного, а другий відхиляється

Перший промінь називається звичайним (0), а другий – незвичайним (е).
У кристалі ісландського шпату існує єдиний напрямок, уздовж якого подвійного заломлення променів не спостерігається. Напрям у кристалі, вздовж якого промінь розповсюджується, не виявляючи подвійного заломлення променів, називається оптичною віссю кристала. Це напрям, а не пряма лінія, що проходить крізь будь-яку точку кристалу. Кожна пряма, яка проходить паралельно даному напрямку, є оптичною віссю кристала.
Площина, яка проходить через промінь і оптичну вісь кристалу, що перетинає промінь, називається головною площиною, або головним перерізом кристалу. Аналіз світла (наприклад, за допомогою турмаліну або скляного дзеркала) показує, що після проходження кристала промені стають плоскополяризованими у взаємно перпендикулярних площинах: коливання світлового вектора (вектора напруженості Е електричного поля) у звичайному промені проходять перпендикулярно до головної площини, а в незвичайному – в головній площині . Неоднакове заломлення звичайного і незвичайного променів вказує на різницю їх показників заломлення. Очевидно, що для будь-якого напрямку звичайного променя коливання світлового вектора перпендикулярні до оптичної осі кристалу, тому звичайний промінь розповсюджується по всіх напрямках з однаковою швидкістю, отже , показник заломлення n0 для нього є сталою величиною. Незвичайний промінь має між напрямком коливань світлового вектора і оптичною віссю кут, відмінний від прямого, який залежить від напрямку променя, тому незвичайні промені розповсюджуються в різних напрямках з різними швидкостями. Отже, показник заломлення ne незвичайного променя є змінною величиною, яка залежить від напряму променя. Таким чином, звичайний промінь підпорядковується закону заломлення (звідси і назва – “звичайний”), а для незвичайного променя цей закон не виконується. Після проходження кристала, якщо не брати до уваги поляризацію у взаємно перпендикулярних площинах, ці два промені не відрізняються один від одного.
4.Поляризаційні призми та поляроїди.

Білет 15

1.

2.

3.Інтерференцією називається явище накладання двох, або кількох когерентних світлових хвиль, в результаті якого відбувається перерозподіл інтенсивності світла в просторі.

Когерентними називаються хвилі з однаковою частотою і сталою різницею фаз, вектори напруженості електричного поля яких коливаються в одній площині.

Умова: інтерференція виникає при розділенні початкового променю світла на два промені при його проходженні через тонку плівку, наприклад плівку, що наносять на поверхню лінз у просвітленних об'єктивах. Промінь світла, проходячи через плівку товщиною , відіб'ється двічі — від внутрішньої та зовнішньої її поверхонь. Відбиті промені матимуть постійну різницю фаз, що дорівнює подвоєній товщині плівки, від чого промені стають когерентними і будуть інтерферувати.

Білет 16

1 )

d²g/dt²+w0²g=0, де ω₀=1/√LC-власна частота контура

Т=2π√LC - період власних коливань формули Томсона

Записавши правила Кіргофа для розглядуваного коливального контура, та закон Ома для вільних незагасаючих електромагнітних коливань

Т=2π/ω_0, Т=1/ν, ω=2πν

Розв*язком цього рівняння є функція: g=g_mcos(ω₀ t+φ₀)

Cила струму в коливальному контурі I=I_max cos(ω₀ t+φ₀+π/2)

Напруга на конденсаторі ν_с=g/c=ν_mcos(ω0 t+φ0)

2)

Об*ємна густина кінетичної енергії середовища ωk=dW_K/dV=1/2ρV²

Об*ємна густина потенціальної енергії пружно-деформованого середовища

ω_п= dW_п/dV=1/2ρV²ε²

Об*ємною густиною енергії пружної хвилі наз. об*ємна густина механічної енергії середовища, обумовлена поширенням цієї хвилі. Об*ємна густина пружної хвилі дор. сумі: ω= ω_k+ ω_п

Середнє за період значення об*ємної густини енергії дор: <ω>=ρA²•ω²

Вектор Умова - вектор густини потоку енергії ͞͞͞͞u=ω͞v

3)

Смугами рівного нахилу наз. диференціальна картина, яка утворюється при падінні світла на паралельну площину фіксованої товщини під однаковими кутами.

Смуги рівного нахилу локалізовані та нескінченні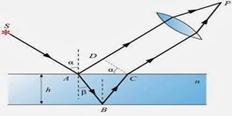

Смуги рівної товщини.

Допустимо, що товщина пластинки не постійна (∼b, n = const).

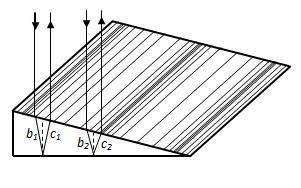Тоді у всіх тих місцях пластинки, де товщина b, а отже, і різниця ходу Δ однакові, спостерігається той самий результат інтерференції. Це означає, що уздовж якої-небудь темної або світлої інтерференційної смуги, що утворюється на поверхні, товщина цієї пластинки та сама.

Смуги рівної товщини локалізовані на поверхні пластинки. При спостереженні в білому світлі смуги будуть пофарбовані так, що поверхня містить усі кольори веселки. Приклад смуг рівної товщини: нафтові плями, мильні плівки і т.д.

Кільця Ньютона - приклад смуг рівної товщини. Вони спостерігаються при відбитті світла. від дотичних одна з одною плоско паралельної товстої скляної пластинки й плоско опуклої лінзи з великим радіусом кривизни. Роль тонкої плівки змінної товщиниb, від поверхні якої відбиваються когерентні хвилі, відіграє зазор між пластинкою й лінзою. Нехай показник заломлення зазору n, товщина в точці Е рівна b. Паралельний пучок світла падає нормально (i₁= 0°) на плоску поверхню ВС лінзи й відбивається від верхньої й нижньої поверхні зазору ( від т. Е і F ).

Білет 17

1.Коливання називаються вільними, якщо вони здійснюються за рахунок енергії, яка була надана, за відсутності в наступному зовнішніх впливів на коливну систему.

гармонічні коливання – коливання, при яких значення фізичної величини змінюється з часом за законом косинуса (синуса)

Нехай матеріальна точка здійснює прямолінійні гармонічні коливання вздовж осі координат 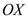біля положення рівноваги, яке прийняте за початок координат. Тоді залежність координатих від часу 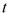задається рівнянням

.

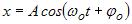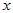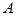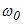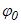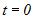Тут – зміщення коливної точки; – амплітуда коливання ; – циклічна частота; – початкова фаза коливань в момент часу ; – фаза коливань в момент часу .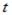

Найменший проміжок часу Т, після проходження якого повторюються значення всіх фізичних величин, що характеризують коливання, називається періодом коливання. За час Тздійснюється одне повне коливання і фаза коливань отримує приріст 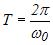., Частотою коливань називається кількість повних коливань, що здійснюються за одиницю часу:

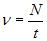
Циклічна частота

2. Ті точки середовища, у яких амплітуда стоячої хвилі максимальна й рівна 2А, називаються пучностями. Координати пучностей можна знайти з умови, що

звідси ,,,,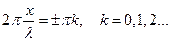

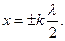
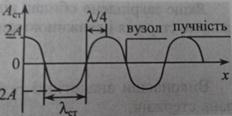
Відстань між двома сусідніми пучностями рівна о .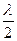

Точки, у яких амплітуда стоячої хвилі мінімальна й рівна 0, називаються вузлами. Координата вузлів можна знайти з умови

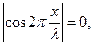звідси ,,,,,,

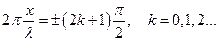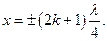
3.Кільця Ньютона - приклад смуг рівної товщини. Вони спостерігаються при відбитті світла. від дотичних одна з одною плоско паралельної товстої скляної пластинки й плоско опуклої лінзи з великим радіусом кривизни. Роль тонкої плівки змінної товщини b, від поверхні якої відбиваються когерентні хвилі, відіграє зазор між пластинкою й лінзою. Нехай показник заломлення зазору n, товщина в точці Е рівна b. Паралельний пучок світла падає нормально (i₁= 0°) на плоску поверхню ВС лінзи й відбивається від верхньої й нижньої поверхні зазору ( від т. Е і F ).

Оптична різниця ходу між променями, відбитими від верхньої й нижньої поверхні зазору рівна

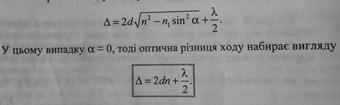
Білет 18

1. Гармонічні коливання – періодичні коливання, які з часом змінюються за гармонічним законом та повертаючи сила змінюються за квазіупружним законом.
Диф. Р-ння
F=F_пов
За 2 законом Ньютона: ma = -kx
ma+kx = 0
md²x/dt² + kx = 0
d²t/dt² + ɷ₀²x = 0 де ɷ — циклічна частота, k — хвильове число.

2. Фазова швидкість — одна із характеристик хвилі, що характеризує поширення збурення будь якої фізичної природи. Поняття фазової швидкості може використовуватись при розповсюдженні збурень будь якої форми, якщо в впроцесі розповсюдження ця форма не змінюється. На рисунку проілюстровано визначення фазової швидкості збурень в струні.

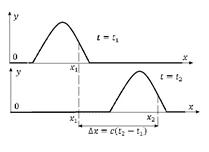
V = √E/ρ V=√G/ρ
Групова швидкість хвиль - швидкість руху групи або низки хвиль, яка за відсутності поглинання в середовищі збігається із швидкістю переміщення енергії цієї групи хвиль.
U = υ – λ* (dυ/dλ)
3. Когереними назив світлові хвилі з однаковою частотою, сталою різницею фаз та для яких коливання векторів напруженостей електричного і магнітного полів відбувається у взаємно перпендикулярних площинах, тобто є впорядкованими.
max: Δ= ±2 k* λ/2 min: Δ= ±(2 k+1)* λ/2
Інтерференцією світла назив. Явище накладання двох або кількох когерентних світлових хвили, в результаті якого відбувається перерозподіл інтенсивності в просторі.
max: Δᵠ = ±2 kπ min: Δᵠ = ±(2 k +1)π