
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Движение Жидкостей по Трубам
Рассматривая движение жидкости в большинстве случаев, можно считать: жидкость абсолютно несжимаема; перемещение одних слоев жидкости относительно других не связано с возникновением сил трения. Такая абсолютно несжимаемая и абсолютно невязкая жидкость называется идеальной.
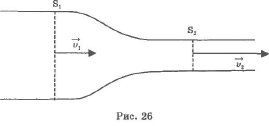
Рассмотрим движение идеальной жидкости по трубе переменного сечения. Так как идеальная жидкость несжимаема, то при установившемся (стационарном) течении через любое сечение ее потока за равные промежутки времени протекают одинаковые объемы жидкости:

При стационарном течении жидкости ее скорость в различных сечениях обратно пропорциональна площади поперечного сечения.
Гидравлические сопротивления.
При течении жидкости по трубам ей приходится затрачивать энергию на преодоление сил внешнего и внутреннего трения. В прямых участках труб эти силы сопротивления действуют по всей длине потока и общая потеря энергии на их преодоление прямо пропорциональна длине трубы. Такие сопротивления называются линейными. Их величина (потеря давления) зависит от плотности и вязкости жидкости, а также от диаметра трубы (чем меньше диаметр, тем больше сопротивление), скорости течения (увеличение скорости увеличивает потери) и чистоты внутренней поверхности трубы (чем больше шероховатость стенок, тем больше сопротивление).
Кроме трения в прямых участках, в трубопроводах встречаются дополнительные сопротивления в виде по-
воротов потока, изменений сечения, кранов, ответвлений и т. п. В этих случаях структура потока нарушается и его энергия затрачивается на перестроение, завихрения, удары. Такие сопротивления называют местными. Линейные и местные сопротивления являются двумя разновидностями так называемых гидравлических сопротивлений, определение которых составляет основу расчета любых гидравлических систем.
Режимы течения жидкости.. В практике наблюдаются два характерных режима течения жидкостей: ламинарный и турбулентный.
При ламинарном режиме элементарные струйки потока текут параллельно, не перемешиваясь. Если в такой поток ввести струйку окрашенной жидкости, то она будет продолжать свое течение в виде тонкой нити среди потока неокрашенной жидкости, не размываясь. Такой режим течения возможен при очень малых скоростях потока. С увеличением скорости выше определенного предела течение становится турбулентным, вихреобразным, при котором жидкость в пределах поперечного сечения трубопровода интенсивно перемешивается. При постепенном увеличении скорости окрашенная струйка в потоке сначала начинает колебаться относительно своей оси, затем в ней появляются разрывы из-за перемешивания с другими струями и затем вследствие этого весь поток получает равномерную окраску.
Наличие того или иного режима течения зависит от величины отношения кинетической энергии потока 1 1
(■п-гпи2=ч-рУи2) к работе сил внут-реннего трения (/•7 = р„5^/)—см. (2.9).
Это безразмерное отношение
^-pVv2/ (р,5^/) можно упростить,
имея в виду, что Ды пропорционально V. Величины / и А/г также
имеют одну и ту же размерность, и их можно сократить, а отношение объема V к поперечному сечению 5 является линейным размером й.
Тогда отношение кинетической энергии к работе сил внутреннего трения с точностью до постоянных множителей можно характеризовать безразмерным комплексом:
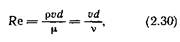
который называется числом (или критерием) Рейнольдса в честь английского физика Осборна Рейнольдса, в конце прошлого века экспериментально наблюдавшего наличие двух режимов течения.
Малые значения чисел Рейнольдса свидетельствуют о преобладании работы сил внутреннего трения в потоке жидкости и соответствуют ламинарному течению. Большие значения Йе соответствуют преобладанию кинетической энергии и турбулентному режиму течения. Граница начала перехода одного режима в другой — критическое число Рейнольдса — составляет 1?екр = 2300 для круглых труб (в качестве характерного размера принимается диаметр трубы).
В технике, в том числе и тепловозной, в гидравлических (в том числе воздушных и газовых) системах обычно имеет место турбулентное течение жидкостей. Ламинарный режим бывает лишь у вязких жидкостей (например, масло) при малых скоростях течения и в тонких каналах (плоские трубки радиатора).
Расчет гидравлических сопротивлений. Линейные потери напора определяются по формуле Дарси-Вейсбаха: 
где X («лямбда») — коэффициент линейного сопротивления, зависящий от числа Рейнольдса. Для ламинарного потока в круглой трубе Я, = 64/Ие (зависит от скорости), для турбулентных потоков величина к мало зависит от
скорости и, главным образом, определяется шероховатостью стенок труб.
Местные потери напора также считаются пропорциональными квадрату скорости и определяются так:

где £ («дзета») — коэффициент местного сопротивления, зависящий от типа сопротивления (поворот, расширение и т. п.) и от его геометрических характеристик.
Коэффициенты местного сопротивления устанавливаются опытным путем, их значения приводятся в справочниках.
Понятие о расчете гидравлических систем. При расчете любой гидравлической системы решается обычно одна из двух задач: определение необходимого перепада давлений (напора) для пропуска данного расхода жидкости или определение расхода жидкости в системе при заданном перепаде давлений.
В любом случае должна быть определена полная потеря напора в системе АН, которая равна сумме сопротивлений всех участков системы, т. е. сумме линейных сопротивлений' всех прямых участков трубопроводов и местных сопротивлений других элементов системы:

Если во всех участках трубопровода средняя скорость течения одинакова, уравнение (2.33) упрощается:
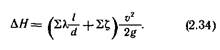
Обычно в системе имеются участки, скорости течения в которых отличаются друг от друга. В этом случае удобно привести уравнение (2.33) к другой форме, учитывая,
что расход жидкости постоянен для всех элементов системы (без ответвлений). Подставив в условие (2.33) значения и = С}/5, получим
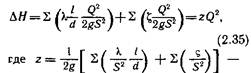
гидравлическая характеристика, или общий коэффициент сопротивления системы.
Необходимо иметь в виду, что расчет трубопроводов не является решением задачи с одним определенным ответом. Его результаты зависят от выбора величины диаметров участков трубопровода или скоростей в них. Действительно, можно принять в расчете невысокие значения скоростей и получить небольшие потери напора. Но тогда при заданном расходе сечения трубопроводов (диаметры) должны быть большими, система будет громоздкой и тяжелой. Приняв высокие скорости течения в трубах, мы уменьшим их поперечные размеры, но при этом существенно (пропорционально квадрату скорости) возрастут потери напора и затраты энергии на работу системы. Поэтому при расчетах обычно задаются какими-то средними, «оптимальными», значениями скоростей течения жидкости. Для водяных систем оптимальная скорость имеет порядок примерно 1 м/с, для воздушных систем низкого давления — 8— 12 м/с.
Гидравлический удар представляет собой явление, происходящее в потоке жидкости при быстром изменении скорости его течения (например, при резком закрытии задвижки в трубопроводе или остановке насоса). В этом случае кинетическая энергия потока мгновенно переходит в потенциальную энергию и давление потока перед задвижкой резко возрастает. Область повышенного давления затем распространяется от задвижки в сторону еще не заторможенного полностью потока со скоростью, близкой к скорости звука а в этой среде.
Резкое повышение давления приводит если не к разрушению, то к упругой деформации элементов трубопровода, что уменьшает силу удара, но усиливает колебания давления жидкости в трубе. Величина скачка давле-
ния при полной остановке потока жидкости, имевшего скорость v, определяется по формуле выдающегося русского ученого — профессора Н. Е. Жуковского, полученной им в 1898 г.: Др = раа, где р — плотность жидкости.
С целью предотвращения ударных явлений в крупных гидравлических системах (например, водопроводных сетях) запорные устройства выполняют так, чтобы их закрытие происходило постепенно.
Диспе́рсная систе́ма — это система, образования из двух или более фаз (тел), которые совершенно или практически не смешиваются и не реагируют друг с другом химически. Первое из веществ (дисперсная фаза) мелко распределено во втором (дисперсионная среда). Если фаз несколько, их можно отделить друг от друга физическим способом (центрифугировать, сепарировать и т. д.).
Обычно дисперсные системы — это коллоидные растворы, золи. К дисперсным системам относят также случай твёрдой дисперсной среды, в которой находится дисперсная фаза.
Диспе́ргатор РПГ- это аппарат, позволяющий диспергировать и получить коллоидный раствор двух и более практически несмешиваемых веществ. Обычно бывают рециркуляционного, встроенного и погружного типа.
Диспе́ргатор аэродинамический- это аппарат, позволяющий диспергировать материалы в газообразной дисперсной фазе.
Наиболее общая классификация дисперсных систем основана на различии в агрегатном состоянии дисперсионной среды и дисперсной фазы. Сочетания трех видов агрегатного состояния позволяют выделить девять видов дисперсных систем. Для краткости записи их принято обозначать дробью, числитель которой указывает на дисперсную фазу, а знаменатель на дисперсионную среду, например для системы «газ в жидкости» принято обозначение Г/Ж.
| Обозначение | Дисперсная фаза | Дисперсионная среда | Название и пример |
| Г/Г | Газообразная | Газообразная | Дисперсная система не образуется |
| Ж/Г | Жидкая | Газообразная | Аэрозоли: туманы, облака |
| Т/Г | Твёрдая | Газообразная | Аэрозоли (пыли, дымы), порошки |
| Г/Ж | Газообразная | Жидкая | Газовые эмульсии и пены |
| Ж/Ж | Жидкая | Жидкая | Эмульсии: нефть, крем, молоко |
| Т/Ж | Твёрдая | Жидкая | Суспензии и золи: пульпа, ил, взвесь, паста |
| Г/Т | Газообразная | Твёрдая | Пористые тела |
| Ж/Т | Жидкая | Твёрдая | Капиллярные системы: жидкость в пористых телах, грунт, почва |
| Т/Т | Твёрдая | Твёрдая | Твёрдые гетерогенные системы: сплавы, бетон, ситаллы, композиционные материалы |
По кинетическим свойствам дисперсной фазы дисперсные системы можно разделить на два класса:
- Свободнодисперсные системы, у которых дисперсная фаза подвижна;
- Связнодисперсные системы, дисперсионная среда которых твердая, а частицы их дисперсной фазы связаны между собой и не могут свободно перемещаться.
В свою очередь эти системы классифицируются по степени дисперсности.
Системы с одинаковыми по размерам частицами дисперсной фазы называются монодисперсными, а с неодинаковыми по размеру частицами — полидисперсными. Как правило, окружающие нас реальные системы полидисперсны.
По размерам частиц свободнодисперсные системы подразделяют на:
| Название | Размер частиц, м |
| Ультрамикрогетерогенные | 10−9…10−7 |
| Микрогетерогенные | 10−7…10−5 |
| Грубодисперсные | более 10−5 |
Ультрамикрогетерогенные системы также называют коллоидными или золями. В зависимости от природы дисперсионной среды, золи подразделяют на твёрдые золи, аэрозоли (золи с газообразной дисперсионной средой) и лиозоли (золи с жидкой дисперсионной средой). К микрогетерогенным системам относят суспензии, эмульсии, пены и порошки. Наиболее распространёнными грубодисперсными системами являются системы «твёрдое — газ», например, песок.
Связнодисперсные системы (пористые тела) по классификации М. М. Дубинина подразделяют на:
| Название | Размер частиц, нм |
| Микропористые | менее 2 |
| Мезопористые | 2-200 |
| Макропористые | более 200 |
По рекомендации ИЮПАК[1] микропористыми называют пористые материалы с размерами пор до 2 нм, мезопористыми — от 2 до 50 нм, макропористыми — свыше 50 нм.
Дата добавления: 2015-01-29; просмотров: 284; Мы поможем в написании вашей работы!; Нарушение авторских прав |