
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение коэффициента гидравлического сопротивления по длине трубопровода при напорном движении жидкости
Цель работы: Определить опытным путем коэффициент Дарси l (коэффициент гидравлического сопротивления) для трубопровода при различных скоростях движения воды. Сравнить значения коэффициентов сопротивлений, полученные из опыта lоп, с вычисленными по соответствующим формулам lт.
1. Основные положения и зависимости
Придвижении жидкости в трубах происходит потеря напора на преодоление сопротивлений движению (следствие работы сил трения).
Потери напора могут быть получены из уравнения Бернулли, где hW – суммарные потери напора между выбранными сечениями, hl – потери напора по длине, hм – потери напора на местные сопротивления:
hW = hl + hм.
Для горизонтального трубопровода постоянного сечения, на котором отсутствуют местные сопротивления, уравнение примет вид
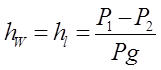 . (6.1)
. (6.1)
Из выражения следует, что можно экспериментально определять потери напора по длине потока, измерив давления Р1 и Р2.
Для вычисления потерь напора по длине при движении жидкости по трубам пользуются формулой Дарси-Вейсбаха:
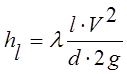 , (6.2)
, (6.2)
где l –безразмерный коэффициент гидравлического сопротивления трению; d – внутренний диаметр трубопровода; V – средняя скорость движения.
Коэффициент гидравлического трения l в общем случае зависит от числа Рейнольдса Re и относительной шероховатости 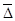 , т.е.
, т.е.
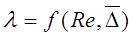 , (6.3)
, (6.3)
здесь 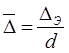 , где DЭ - эквивалентная шероховатость.
, где DЭ - эквивалентная шероховатость.
При ламинарном режиме движения жидкости (Re < 2320) l зависит только от числа Re и определяется по формуле Стокса
l = 64/Re (6.4)
При турбулентном режиме движения существуют три зоны, в которых законы сопротивления различны.
Первая зона называется зоной гидравлически гладких труб (или зона Блазиуса). Здесь l зависит только от числа Re и определяется по формуле Блазиуса
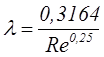 . (6.5)
. (6.5)
Эта формула применима для чисел Reпр1 > Re > 2320, где Reпр1- первое предельное число Рейнольдса, которое может быть определено по формуле
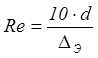 (6.6)
(6.6)
Вторая зона – зона смешанного трения. Здесь l зависит как от числа Re, так и от относительной шероховатости D. Для этой зоны можно пользоваться формулой Альштуля (или любой другой для данной зоны)
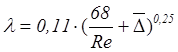 . (6.7)
. (6.7)
Эта формула применима для чисел: Reпр1 < Re < Reпр2, где Reпр2 - второе предельное число Re, которое может быть определено по формуле
 . (6.8)
. (6.8)
Третья зона – зона вполне шероховатых труб, когда Re > Reпр2. Здесь l зависит только от относительной шероховатости D и определяется по формуле Шифринсона
 (6.9)
(6.9)
Дата добавления: 2015-04-18; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |