Простой трубопровод.

Основным элементом любой трубопроводной системы, какой бы сложной она ни была, является простой трубопровод. Классическим определением: простым трубопроводом является трубопровод, собранный из труб одинакового диаметра и качест­ва его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений.

При напорном движении жидкости простой трубопровод работает полным сечением S=4πR²= const. Размер сечения трубопровода (диаметр или ве­личина гидравлического радиуса), а так­же его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками тру­бопровода являются расход жидкости в трубопроводе Q и напор (на головных сооруже­ниях трубопровода, т.е. в его начале). Большинство других характеристик простого тру­бопровода являются, не смотря на их важность, производными характеристиками. По­скольку в простом трубопроводе расход жидкости транзитный (одинаковый в начале и конце трубопровода), то средняя скорость движения жидкости в трубопроводе постоянна v=const. Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези: v=C√Ri, где: - скоростной коэффициент Шези, R_г= S/П - гидравлический радиус сечения, для круглого сечения при полном заполнении жидкостью R_г=d/4; i=h_тр/l - гидравлический уклон. Полагая, что весь имеющийся напор на головных сооружениях (в начале) трубопро­вода тратится на преодоление сил трения в трубопроводе (в простом трубопроводе это по­тери напора по длине ), уравнение движения жидкости (Бернулли) примет вид: H=n²l/CR_г.

Расход жидкости в трубопроводе: Q=v×S = CS√Ri .

Обозначив: SC√R=K , получим основное уравнение простого трубопровода: Q=K√i.

где: К - модуль расхода - расход жидкости в русле заданного сечения при гид­равлическом уклоне равном единице (иначе модуль расхода называют расходной характе­ристикой трубопровода). Другой и более известный вид основного уравнения простого трубопровода получим, решив уравнение относительно напора: H=Q²/K² или H=R×Q²

Величину 1/K² называют удельным сопротивле­нием трубопровода, R=1/Q²- - его полным сопротив­лением

График уравнения простого трубопровода 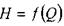носит название его гидравлической харак­теристики. Вид гидравлической характеристики зави­сит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).

Если на трубопроводе собранном из труб одинакового диаметра имеются местные сопротивления, то такой трубопровод можно привести к простому трубопроводу эквива­лентной длины l_экв: l_экв = l +d∑ξ /λ.

Обобщенное уравнение Бернулли для одномерного течения как механическая форма уравнения энергии и его развернутое толкование для несжимаемой. (капельной) жидкости и для газа. Коэффициент Кориолиса.

В общем случае движение жидкостей и газов сопровождается выполнением внешней механической работы, хотя понятие внешней работы широко, оно включает ту составляющую работы сил трения, которая идёт на увеличение E_k жидкости и дислинация которой не происходит.

Обобщенное уравнение Бернулли: , где l_ТР - работа сил трения, l - техническая работа

,

, , ,

;

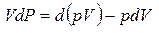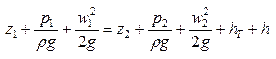
h – изменение напора при совершении технической работы.

h_T – изменение напора при преодолении сопротивления.

При неравномерном распределении скоростей вводится к-т Кориолиса – к-т неравномерности поля скоростей, к-т Кориолиса – это отношение действ. кин. энергии потока к кинет. энергии потока с тем же расходом, не имеющего равномерное поле скоростей в том же сечении.

При турбулентном режиме течения , при ламинарном . . .

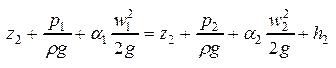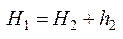
При 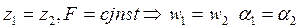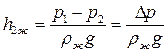, (м)

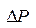- потери давления, поэтому вместо можно записать .

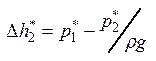
Уравнение Бернулли для одномерного течения идеальной несжимаемой жидкости как механическая форма уравнения энергии и его развернутое толкование. Гидростатический закон распределения давления в поперечном сечении одномерного потока.

Уравнение Бернулли определяет изменение основных параметров - и высоты положения жидкости. Для несжимаемой жидкости

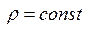
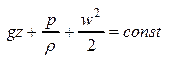или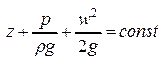

z – геометрич-я высота (напор) 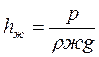- полн мех-кая энергия жид-ти или напор составляющие полной мех. энергии жидкости: - потенциальная энергия положения жидкости, или геомерт. напор.

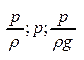- потенц энергия давления жид-ти или пьезометрический напор.

- потенциальная энергия жидкости или динамический напор. Энергетический смысл уравнения Бернулли заключается в утверждении закона сохранения полной механической энергии единицы массы несжимаемой жидкости.

Геометрическую высоту z можно отсчитывать от оси горизонтального канала

при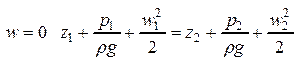

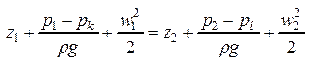
- избыточное давление.

Для измерения кинетической энергии используется трубка полного давления. Давление торможения (полное).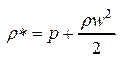

Постоянство трёх постоянных справа означает, что они могут взаимно превращаться и их сумма постоянна – это условие гидростатического равновесия жидкости..

Увеличение скорости несжимаемой жидкости в горизонт. струйке всегда сопровождается уменьшением давления, а уменьшение скорости – увеличением давления вплоть до p* при w=0.