
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет кривой свободной поверхности на быстротоке
Исследуя дифференциальное уравнение неравномерного движения в призматических руслах
= , (2.22)
где Пк – параметр кинетичности, сделать вывод о типе и форме кривой свободной поверхности на быстротоке.
Рассчитать кривую свободной поверхности на водоскате быстротока.
Существует несколько методов расчета: Б.А. Бахметева, метод академика Н.Н. Павловского и другие в практике дорожно-мостового b аэродромного строительства приходится решать задачи по расчету неравномерного плавноизменяющегося движения воды не только в призматических руслах, но и на непризматических участках каналов. Поэтому предлагается студентам воспользоваться универсальным методой конечных разностей, предложенным В.И. Чарномскин.
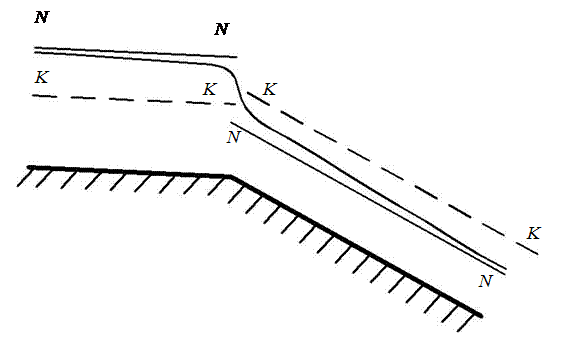 |
Рис. 2.9
Метод В.И. Чарномского заключается в следующем: зная глубину в одном из сечений канала, например глубину на изломе дна подводящего канала и лотка быстротока hn = hизл, задаемся значением глубины в соседнем сечении hn+1 и находим искомое расстояние Δl между двумя соседними сечениями с известными глубинами по уравнению
Δl = , (2.23)
где ΔЭ – изменение удельной энергии сечения в пределах выбранного участка; iтр – уклон трения (среднее значение гидравлического уклона в пределах рассматриваемого участка).
Для удобства расчет сводится в табл. 2.6.
Сложность заполнения таблицы заключается в том, что определяемые величины подразделяются на построчные и междустрочные. В табл. 2.6 знаком "–" указано место положения определяемой величины. Так, построчными значениями являются ω, χ, R, …, соответствующие назначенной глубине h, а междустрочными – R¯, C¯, ..., определяемые как среднеарифметические или по соответствующим формулам.
Таблица 2.6
| h | ω | χ | R | R¯ | C | C¯ | υ | υ¯ | iтр | Э | ΔЭ | Δl | l |
| h1 | – | – | – | – | – | – | |||||||
| – | – | – | – | – | – | ||||||||
| h2 | – | – | – | – | – | – | – | ||||||
| – | – | – | – | – | – | ||||||||
| h3 | – | – | – | – | – | – | |||||||
| … ... … … | |||||||||||||
| hn | – | – | – | – | – | – | – |
Приведем необходимые для расчета понятия и формулы с нумерацией по столбцам.
1) h1 = hизл – последняя глубина на быстротоке принимается на 5% больше нормальной глубины, т.е. hn = 1,05 · h02; промежуточные глубины рекомендуется задавать с интервалом 0,1 м, опираясь на удобные при последующем построении числовые значения глубин (например, h2 = 1,1; 1,0;0,9;…);
2) ω = b · h, т.к. лоток прямоугольной формы и коэффициент откоса m = 0;
3) χ = b + 2· h, т.к. лоток прямоугольной формы в коэффициент
откоса m = 0;
4) R = ω / χ;
5) R¯ = , где Rn и Rn+1 - гидравлические радиусы, соответствующие соседним глубинам;
6) С = · R 0,2, где nа – коэффициент шероховатости с учетом аэрации потока;
7) C¯ = , где Cn и Cn+1 – коэффициенты Шези, соответствующие соседним глубинам;
8) υ = Q0 / ω, где Q0 – заданный расход воды, поступающий из подводящего канала;
9) υ¯ = , где υ n и υ n+1 – средние скорости в соседних сечениях;
10) iтр = ;
11) Э = h + , где Э – удельная энергия соответствующих сечений;
12) ΔЭ = Эn+1 – Эn где Эn+1 и Эn – удельные энергии соседних
сечений, причем в последующем сечении для данного типа кривой спада
удельная энергия сечения больше, чем в предыдущем;
13) Δl = ;
14) l1 = 0, т.к. расчет кривой свободной поверхности начинается с точки излома дна; последующие числовые значения длин l2, l3 , … определяются путем наращивания, а именно: l2 = l1 + Δl1, l3 = l2 + Δl2и т.д.
Дата добавления: 2015-04-18; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |