Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли является одним из основных уравнений гидродинамики, выражает частный случай закона сохранения энергии для потока движущейся жидкости. Для установившегося плавно изменяющегося потока реальной жидкости, для двух произвольно выбранных сечений уравнение Бернулли имеет вид:

(2.7)

где z – удельная энергия положения, возвышение рассматриваемых живых сечений над плоскостью сравнения;

– удельная потенциальная энергия давления или пьезометрический напор, соответствующий абсолютному или манометрическому давлению жидкости;

– удельная потенциальная энергия жидкости или потенциальный напор;

– удельная кинетическая энергия или скоростной напор;

– потери напора на преодоление гидравлических сопротивлений
между сечениями.

Все члены уравнения (2.7) имеют размерность длины и поэтому его можно изобразить графически (рис. 2.1).

Рис. 2.1

Отношение потерь напора на участке 1-2 к длине этого рукава , измеренного по оси потока, называется гидравлическим уклоном:

(2.8)

Решение задач с использованием уравнения Бернулли рекомендуется проводить в следующей последовательности:

а) выбрать два сечения, которые будут соединяться уравнением Бернулли. Необходимо выбрать сечения, для которых известно возможно большее число гидродинамических элементов, а также сечения, для которых гидродинамические элементы необходимо определить;

б) выбрать горизонтальную плоскость сравнения. Её необходимо выбирать таким образом, чтобы z₁ или z₂, входящие в уравнение Бернулли, обратились в нуль;

в) записать уравнение (2.7) для двух выбранных сечений;

г) установить значение величин, входящих в уравнение Бернулли;

д) подставить найденные значения слагаемых в уравнение Бернулли и определить искомую величину.

Задачи

2.20. Определить предельную высоту расположения центробежного насоса над уровнем воды в водоисточнике (рис. 2.2), если насос забирает воду в количестве 30 л/с, диаметр всасывающей трубы 150 мм. Вакуумметрическое давление, создаваемое во всасывающем патрубке, составляет 6,5×10⁴ Па, потери напора во всасывающей линии 1 м.

Рис. 2.2

Решение. Выбираем два сечения: I-I по оси насоса и О-О – по линии свободной поверхности воды. Сечение О-О совпадает с плоскостью сравнения. Уравнение Бернулли для сечений О-О и I-I будет иметь вид:

В сечении О-О скорость , поэтому скоростной напор

Давление на свободной поверхности равно атмосферному
тогда пьезометрический напор

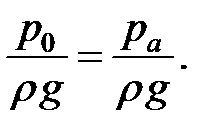
Плоскость сравнения совпадает с сечением О-О, поэтому

Абсолютное давление в сечении I-I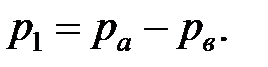

Тогда

Высота расположения оси насоса над уровнем воды в водоисточнике определится из уравнения

Скорость движения воды во всасывающей трубе

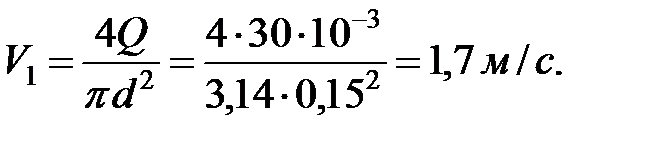
Скоростной напор

Вакуумметрическая высота

Тогда

2.21. Определить вакуумметрическое давление, которое должен создать центробежный насос во всасывающей трубе диаметром 100 мм при расходе 20 л/с (рис. 2.2). Возвышение оси насоса над поверхностью воды составляет 5 м, потери напора во всасывающей линии 0,85 м.

2.22. Определить с какой максимальной высоты центробежный насос пожарного автомобиля может забрать воду из водоёма, если подача насоса 35 л/с, диаметр всасывающего рукава 150 мм. Вакуумметрическое давление во всасывающем патрубке 8×10⁴ Па.

2.23. Построить пьезометрическую линию и линию изменения гидродинамического напора для пожарного ствола диаметром 50 мм с насадком диаметром 13 мм. Расход составляет 3 л/с. Построение произвести в масш-табе после определения пьезометрического и скоростного напора в сечениях I-I и II-II(рис. 2.3). Избыточное давление в сечении I-I составляет 2,8×10⁵ Па.

Рис. 2.3

2.24. Вода в количестве 10 л/с подается в эжектор при помощи центробежного насоса, создающего перед соплом избыточное давление 4,7×10⁵ Па. Определить с какой высоты можно поднять воду из резервуара, расположенного ниже оси эжектора (рис. 2.4). Диаметр подводящей трубы d₁ = 70 мм, диаметр сопла d₂ = 20 мм. Потерями напора пренебречь.

Рис. 2.4

2.25. По данным задачи 2.24 построить пьезометрическую и напорную линии. Построение произвести в масштабе для сечений I-I и II-II.

2.26. Определить разряжение в вакуумной камере стационарного пеносмесителя ПС-5 пожарного насоса ПН-40У, имеющего входное сечение диаметром 30 мм и выходное (сопло) диаметром 16,3 мм (рис. 2.5).

Расход воды 6 л/с, напор у пеносмесителя 45 м.

Рис. 2.5

2.27. Определить расход воды через сопло пеносмесителя ПС-5, имеющего входное сечение диаметром 30 мм и выходное (сопло) диаметром 16,3 мм (рис. 2.5). Величина вакуума составляет 3,5 м. Давление перед
пеносмесителем 4×10⁵ Па.

2.28. Манометр, установленный на стволе-водомере, показывает давление 3,8 ат (рис. 2.6). Диаметр насадка 25 мм. Определить скорость и расход воды. Потерями напора пренебречь.

Рис. 2.6

2.29. Определить какое избыточное давление должно быть у ствола с насадком 22 мм, чтобы расход воды составил 10 л/с. Потерями напора пренебречь.

2.30. Определить необходимое избыточное давление у ствола с насадком диаметром 19 мм, чтобы скорость на выходе из насадка составил 30 м/с.

2.31. Как изменится расход жидкости через пожарный ствол, если давление перед ним упало в 2 раза.

2.32. Определить скорость выхода воды из насадка пожарного ствола при напоре 35 м, если при напоре 30 м скорость составляет 25 м/с.

2.33. Определить расход воды из насадка пожарного ствола при напоре 30 м, если при напоре 25 м расход воды составляет 8 л/с.

2.34. При испытании внутреннего пожарного крана на водоотдачу использовалась трубка Пито (рис. 2.7). Манометр, установленный на трубке Пито, показал давление 3 ат. Определить, пренебрегая потерями напора, скорость струи и расход через насадок диаметром 16 мм.

Рис. 2.7

2.35. Сравнить скорость струи и расход воды из стволов с насадками 13 мм и 16 мм, если манометр, установленный на трубке Пито, показал одинаковое давление 2,5 ат.

2.36. Для заполнения пожарного водоёма используется трубопровод длиной 600 м. Определить необходимый напор насоса, если возвышение водоёма над источником составляет 15 м, гидравлический уклон 0,03, свободный напор в конце линии 5 м.

2.37. Определить гидравлический уклон трубопровода длиной 500 м (рис. 2.8), если манометры, установленные в начале и в конце трубопровода, показали давление 4,5 ат и 3,6 ат соответственно, возвышение осей манометров над плоскостью сравнения: z₁ = 2 м; z₂ = 6 м.

Рис. 2.8

2.38. Определить на какую высоту h сможет подняться вода из резервуара по трубе, присоединенной к узкому сечению трубопровода диаметром 50 мм (рис. 2.9), если расход воды по трубопроводу 10 л/с. Диаметр трубопровода 100 м. Избыточный напор перед сужением 0,6 м. Потерями напора пренебречь.

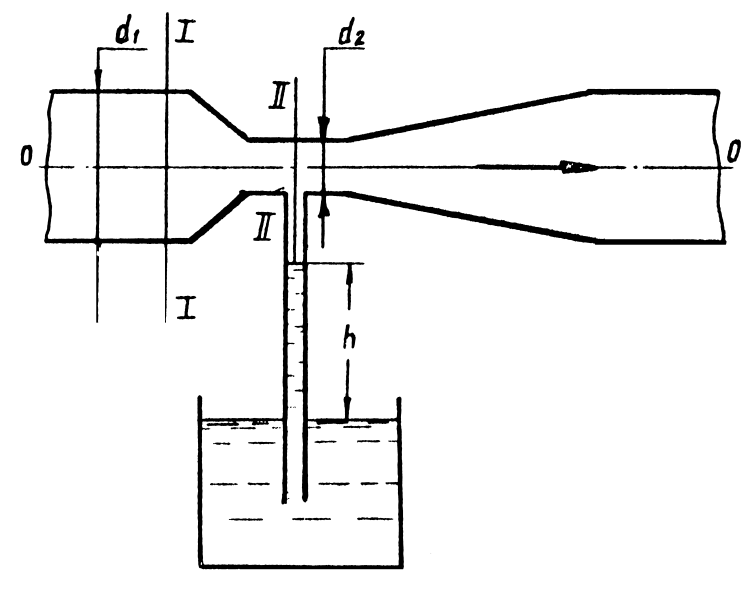
Рис. 2.9

2.39. Определить диаметр узкого сечения трубопровода (рис. 2.9), чтобы при расходе 15 л/с по трубопроводу диаметром 125 мм, высота подъёма воды из резервуара составляла 80 см. Избыточное давление перед сужением 10 кПа. Потерями напора пренебречь.

2.40. Определить расход воды по трубопроводу диаметром 200 мм, имеющем сужение диаметром 50 мм (рис. 2.9), чтобы обеспечить подъём воды из резервуара на высоту 3,1 м. Избыточное давление перед сужением 12 кПа. Потерями напора пренебречь.

2.41. Определить среднюю скорость движения воды, если разность высот подъёма воды в пьезометре и скоростной трубке составляет 60 см (рис. 2.10).

Рис. 2.10

2.42. Определить разность уровней в скоростной трубке и пьезометре (рис. 2.10), если скорость движения воды на уровне центров входных сечений трубок равна 2,3 м/с.

2.43. Определить расход воды по показаниям пьезометрического водомера (рис. 2.11). Диаметр трубы D = 50 мм, диаметр суженого сечения
d = 25 мм, разность пьезометрических высот 100 см.

Рис. 2.11

2.44. Определить расход воды через пьезометрический водомер (рис. 2.11), если D = 200 мм, d = 100 мм. Разность пьезометрических высот 60 см.