
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос №54. Корреляционно-регрессионный метод анализа
Исследование объективно существующих связей между явлениями – важнейшая задача в процессе принятия решений.
Этапы анализа взаимосвязи случайных величин:
1)качественный анализ явления, связанный с анализом его природы методами экономической теории, социологии, конкретной экономики;
2)построение модели связи;
3)интерпретация результатов.
В статистике различают функциональную связь, и стохастическую зависимость. Функциональнойназывают такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической.Частным случаем стохастической связи является корреляционнаясвязь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. Теснота связи может определяться коэффициентом корреляции.
Коэффициент корреляции r – это безразмерная величина, изменяющаяся от –1 до 1, показывающая тесноту связи и ее направление. Связь может быть прямая, r>0 (когда с возрастанием факторного признака возрастает и результативный) и обратная, r<0.
Существует несколько формул для вычисления коэффициента корреляции, вот одна из них:

По степени тесноты связи различают количественные критерии оценки тесноты связи (табл. 1).
Т а б л и ц а 1
| Величина коэффициента корреляции | Характер связи | |||
До 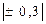
| практически отсутствует | |||
| Величина коэффициента корреляции | Характер связи | |||

| слабая умеренная сильная | |||
1. Высокий коэффициент корреляции ( выше +0.9 или ниже –0.9) показывает сильную связь между величинами (рис 1 а-г).
 |
2. Маленький коэффициент корреляции (близкий к 0) не всегда отражает отсутствие связи между величинами. Он лишь показывает отсутствие линейной зависимости (рис 1 д,е).
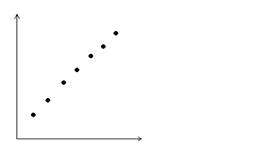 |
Рис. 1а. Совершенная поло- Рис.1б. Совершенная отрицательная
жительная корреляция , r=1, корреляция, r = -1,
 |
функциональная связь функциональная связь
Рис. 1в. Сильная положительная Рис. 1г. Сильная отрицательная
 |
корреляция, r ≈0,9 корреляция, r ≈ - 0,9
Рис.2.10е. Отстутствие линейной зависимости, r=0, но есть
параболическая зависимость.
Если две величины являются коррелированными, то дисперсия их суммы вычисляется так:
 ,
,
где 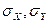 – стандартные отклонения для X и Y.
– стандартные отклонения для X и Y.
Очевидно, что если величины X и Y некоррелированы, то r=0,и формула сложения дисперсий принимает вид:
 .
.
Дата добавления: 2015-04-18; просмотров: 230; Мы поможем в написании вашей работы!; Нарушение авторских прав |