Основные теоретические сведения. Экспериментальные исследования показали, что затраты энергии на преодоление гидравлических сопротивлений

Экспериментальные исследования показали, что затраты энергии на преодоление гидравлических сопротивлений, процессы тепло- и массообмена существенно зависят от режимов движения жидкостей (газов). Изучение режимов движения и закономерностей, их определяющих, имеет большое практическое значение.

Используя жидкость, пропускаемую по прозрачному трубопроводу, можно установить наличие двух режимов течения - ламинарного и турбулентного. Обычно при малых скоростях элементарные струйки жидкости движутся параллельно, не перемешиваясь. Такое движение жидкости называется ламинарным или слоистым (вязкостным). Силы вязкости, возникающие между слоями при движении, подавляют пульсации скорости отдельных частиц и препятствуют переходу в соседние слои.

При больших скоростях возникают поперечные пульсации скоростей и давлений, вызывающие интенсивное перемешивание струек жидкости. Такой вид движения называется турбулентным.

Для ламинарного течения жидкости характерен параболический закон распределения скоростей по поперечному сечению трубопровода (рис.1). При этом средняя скорость жидкости составляет 0,5 от максимальной скорости на оси потока.

Распределение скоростей при турбулентном течении в ядре потока более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении (рис.2).

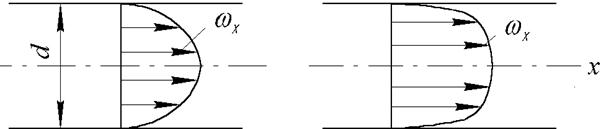
Средняя скорость жидкости для турбулентного режима составляет 0,8-0,9 от максимальной на оси потока.

Режим движения жидкости зависит не только от скорости потока, но и от геометрических размеров потока (эквивалентного диаметра), вязкости и плотности жидкости.

Эквивалентным диаметром называется диаметр d_э, выраженный через гидравлический радиус. Гидравлический радиус R_г - отношение "живого" сечения потока F_ж.с. к его смоченному периметру П.

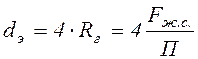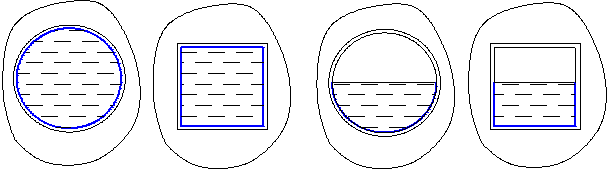
Рисунок 3 – К определению эквивалентного диаметра

-------------- - периметр канала, – смоченный периметр.

Для трубы круглого сечения при её полном заполнении d_э=d.

Влияние перечисленных физических параметров потока на режим движения жидкости описывается критерием (числом) Рейнольдса:

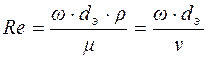где w - средняя скорость потока, м/с;

d_э - эквивалентный диаметр трубопровода, м;

r - плотность жидкости, кг/м³;

n=m/r - кинематический коэффициент вязкости, м²/с;

μ – динамический коэффициент вязкости, Па∙с.

Критерий Рейнольдса показывает отношение сил инерции, характеризующихся скоростью потока и его размерами к силам внутреннего трения, обусловленными вязкостью потока. При больших скоростях (больших числах Re) силы инерции превосходят силы вязкости и не препятствуют пульсациям скорости и перемешиванию жидкости, что соответствует турбулентному течению. При малых скоростях (малых числах Re), наоборот, силы внутреннего трения преобладают над силами инерции и гасят пульсации скорости - жидкость движется ламинарно (слоисто).

Переход от ламинарного течения к турбулентному происходит при определённом значении числа Re, которое в этом случае называется критическим. Как показывают опыты, для труб круглого сечения Re_кр=2300.

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re<Re_кр течение является ламинарным, при Re>Re_кр - турбулентным. Вполне развитое турбулентное течение в трубах устанавливается при Re=4000, а при Re=2300¸4000 имеет место переходная область.

Потери напора h_тр по длине трубы при ламинарном движении пропорциональны первой степени скорости:

,

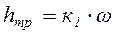где к₁ - коэффициент пропорциональности, зависящий от размеров трубы и свойств жидкости.

При развитом турбулентном режиме потери h_тр пропорциональны квадрату скорости:

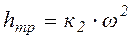где к₂ - коэффициент, в общем случае зависящий от числа Re и шероховатости стенки трубы.

В переходной области сопротивления, когда касательные напряжения в потоке, вызванные вязкостью жидкости, соизмеримы с напряжениями от пульсации скорости, потери напора h_тр пропорциональны скорости в степени m, где 1 £ m £ 2.