ОПРЕДЕЛЕНИЕ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ ТРУБОПРОВОДОВ

Цель работы: опытное определение коэффициентов гидравлического сопротивления и их сравнение с табличными или расчётными данными.

Гидродинамический напор идеальной жидкости описывается уравнением Бернулли:

, (1)

где w²/2g — скоростной или динамический напор, м;

p/ρg — статический или пьезометрический напор, м;

z — геометрический напор или нивелирная высота, м.

Движение реальных текучих сред отличается от движения идеальных жид­костей наличием сопротивления движению, обусловленным силами внутрен­него трения между элементарными слоями и струйками среды. По условию неразрывности потока его расход, а следовательно, и динамический напор остаются неизменными по длине трубопровода. Кроме того, для трубопровода постоянного сечения w = const. Поэтому гид­равлическое сопротивление трубопровода уменьшает полный напор за счет уменьшения его статической составляющей p/ρg.

Движение реальных жидкостей в горизонтальных каналах характеризуется уравнением Бернулли (при z₁=z₂):

, (2)

где

∆p_сопр=ζρw²/2 — гидравлическое сопротивление участка трубопровода между двумя сечениями;

ζ — коэффициент сопротивления.

Знание ζ позволяет рассчитывать сопротивление технологических коммуникаций и аппаратов, что необходимо для определения параметров трубопроводов, выбора насоса, расхода энергии на транспортирование среды.

Общее гидравлическое сопротивление коммуникаций и аппаратов складывается из сопротивления трения и местных сопротивлений при изменении геометрической формы трубопроводов. Рассмотрим отдельно каждое из них.

А. Сопротивление трения

При ламинарном течении среды зависимость между потерями давления на трение и определяющими его факторами описывается законом Гагена-Пуазейля:

, (3)

где μ — динамическая вязкость, Па∙с;

w — средняя скорость потока, м/с;

d — диаметр трубопровода, м;

l — длина, м.

Из уравнения (3) после некоторых преобразований получается уравнение Дарси:

, (4)

где ζ=λl/d — коэффициент сопротивления трения, λ — коэффициент гидравлического трения. Сопоставляя уравнения (3) и (4), получим:

(5)

Коэффициент гидравлического трения или просто коэффициент трения при турбулентном режиме аналитически рассчитать нельзя. Исследования показали, что для гладких труб в области значений 2300 < Re < 100 000 он может быть определен по формуле Блазиуса:

(6)

а в пределах значений 100 000 < Re < 100 000 000 из выражения

, (7)

Б. Местные сопротивления

Местные сопротивления связаны с изменением геометрической формы потока (скорости или направления) при поворотах, при прохождении через участки резкого или плавного расширения, при сужениях в кранах, задвижках, вентилях и т.д.

Потери полного напора на местные сопротивления проявляются за счет уменьшения его статической составляющей, выраженной в метрах столба текучей среды или в единицах давления. Они, как и потери на трение (см. уравнение 4), выражаются в долях динамического напора.

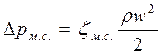, (8)

где ζ_м.с. — коэффициент местного сопротивления.

При резком расширении трубопровода скорость w₂ в широком сечении оказывается меньше скорости w₁ в узком сечении во столько раз, во сколько раз площадь широкого сечения больше площади узкого сечения. При этом происходит как бы наталкивание узкой струи на более медленную широкую, поэтому условно здесь можно говорить о столкновении ударного характера. Исходя из теоремы механики о кратковременном действии сил при ударе, французский ученый Борд показал, что величина потерь напора при внезапном расширении может быть описана выражением:

, (8а)

где

Потеря напора в месте внезапного расширения происходит за счет вихреобразования в периферийной части потока А (рисунок 1). На это расходуется часть энергии жидкости.

Рисунок 1- Внезапное расширение

Рисунок 2- Внезапное сужение

При внезапном сужении трубопровода (рисунок 2) в кольцевом пространстве А (застойная зона) происходит образование вихревых движений. Кроме того, вследствие сужения струи и в малом сечении трубопровода (S₂) образуются вихри в области А₁. «Самосужение» струи в сечении S₃ объясняется инерционными силами потока, которые в непосредственной близости от узкого сечения сходятся к оси трубопровода. Опыты показывают, что основные потери энергии происходят в области А₁. определение потерь производится в этом случае по выражению:

, (8б)

где w₂ — скорость потока в узком сечении, м/с.

Коэффициенты местных сопротивлений для кранов, вентилей и др. также определяются опытным путем и зависят от конструкции запорного устройства.

В настоящей работе необходимо:

1. определить опытное значение λ_оп для прямого участка трубопровода и сравнить его с λ_теор, рассчитанным по одной из формул (5) или (7) в зависимости от значения числа Re;

2. определить опытные значения коэффициентов местных сопротивлений.