Общие сведения. Нахождение потерь напора (удельной механической энергии) при дви­жении жидкостей составляет одну из основных задач практической гидравлики

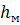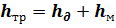
Потери напора по длиневызваны тормозящим действием стенок, приво­дящим к вязкостному трению частиц и струек жидкости друг о друга вдоль трубопровода. Такие потери при равномерном течении пропорциональны дли­не потока и для круглых труб (каналов) определяются по формуле Дарси-Вейбаха

(5.1)

где - коэффициент гидравлического трения или коэффициент Дарси;

l,d - соответственно длина и внутренний диаметр трубы (канала);

V- средняя скорость потока.

На рис. 5.1 в логарифмических координатах представлены результаты опытов К. Кольбрука по исследованию гидравлического сопротивдения техни­ческих труб. Из рисунка видно, что коэффициент трения в общем случае зави­сит от числа Рейнольдса Rе и относительной шероховатости стенок трубы 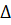/d (где 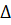- средняя высота выступов шероховатости стенок или абсолютная шеро­ховатость).

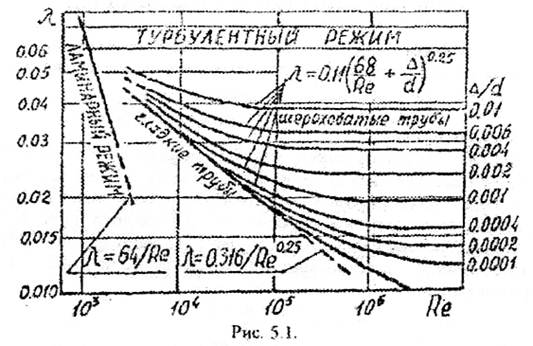
При ламинарном режиме(при Rе<2300) коэффициент трения вычис­ляется по теоретической Формуле Ж. Пуазейля]по которой на графике построена линия ламинарного режима

,

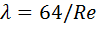Подставляя это значение для в формулу (5. 1) и расписывая число Рсйнольдса Rе = Vd/ 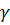, получаем, что в ламинарном потоке потери напора по длине пропорциональны средней скорости в первой степени ( )

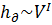При турбулентном режиме течения различают области гидравлически гладких и шероховатых труб (стенок).

Трубу или стенку считают гидравлически гладкой, если соблюдается условие

2300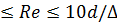

В этом случае прилегающий к стенке ламинарный подслой турбулентного потока покрывает выступы шероховатости и поток не испытывает дополнительных завихрений от шероховатости. По этому в области гидравлически гладких труб, как и в ламинарном режиме, 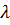зависит только от числа Рейнольдса и вычисляется по эмпирической формуле Г. Блазиуса

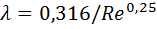
По этой формуле на рис. 5. 1 построена наклонная нижняя прямая описывающая область гладких труб до Re = . Подставляя выражения для 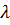в формулу (5.1), легко показать, что в этой области .

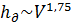С увеличением числа Рейнольдса, например, за счёт повышения скорости течения толщина ламинарного подслоя турбулентного потока уменьшается и при

Re>10d/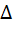

Выступы шероховатости оголяются. Они начинают вносить дополнительные возмущения (вихри) в турбулентное ядро потока, что приводит к возрастанию потерь напора; в этом случае труба (стенка) называется гидравлически шероховатой. Область шероховатых труб представлена на графике семейством кривых, находящихся правее линии гладких труб и описываемых формулой А. Д. Альтшуля

Формула указывает на увеличение коэффициента трения 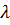с возрастанием относительно шероховатости 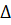/d стенок. При достаточно больших числах Рейнольдса Re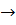 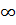, когда практически отсутствует ламинарный подслой, коэффициент 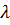не зависит от Re. Он определяется лишь относительной шероховатостью стенок и поэтому кривые графика переходят в горизонтальные прямые, а потери напора по длине становятся пропорциональными квадрату средней скорости ( ). Эту часть области шероховатых труб называют зоной квадратичного сопротивления .

Итак, для нахождения потерь напора по длине необходимо предварительно выявить область сопротивления (область ламинарного движения, область гладких или область шероховатых стенок турбулентного движения), а затем определять коэффициент трения по соответствующим этим областям формулам. Потери напора в трубах не круглого сечения можно определять по формулам для круглых труб, подставляя в них вместо геометрического гидравлический диаметр d=

Вышеприведенные формулы пригодны для вычисления коэффициента трения при равномерном течении, которое устанавливается в трубе (канале) постоянного сечения на некотором расстоянии от входа. Участок, предшествующий наступлению равномерного движения жидкости, называется начальным(разгонным). Он характеризуется повышенными потерями напора, что объясняется неравномерностьютечения из - за изменения эпюры скоростей (не смотря на постоянство средней скорости) по пути. Так, например, на входе из резервуара в трубу частицы жидкости имеют одинаковую по сечению скорость, а по мере удаления от входа, замедляются у стенок и ускоряются около оси потока. Переформирование эпюры скоростей сопровождаются дополнительным расходом энергии и завершается в конце начального участка. Длина начальных участков и потери напора на них определяются по специальным формулам, приведённым в справочной литературе по гидравлике.

В общем случае потери напора в ходе опыта определяются разностью полных напоров на концах рассматриваемого участка потока. Однако при равномерном движении кинетический напор не изменяется по пути и по этому потери напора равны разности только пьезометрических напоров, то есть находятся как разность показаний пьезометров, установленных на конца опытного участка канала (трубы).