Общие сведения. Местные потери напораэнергии жидкости возникают на коротких участках трубопровода с препятствиями для потока

Местные потери напораэнергии жидкости возникают на коротких участках трубопровода с препятствиями для потока, называемыми местными сопротивлениями. К местным гидравлическим сопротивлениямотносятся внезапное расширение и сужение труб, вентили, задвижки, клапаны, колена, решетки, сетки и другие элементы гидросистем, изменяющие конфигурацию стенок трубы или канала. Местные сопротивления вызывают изменение скорости движения жидкости по величине и направлению, что почти всегда приводит к отрыву потока транзитной струи от стенок и возвратному течению жидкости около них, т.е. к образованию циркуляционных зон(рис.6. 1, а). Механическая энергия потока, поглощаемая циркуляционными зонами для создания и поддержания вращения жидкости, составляет, в основном, местные потери напора (механической энергии).

Величинами местных потерь напора экспериментально определяется разность полных напоров жидкости до и после местного сопротивления. Например, потери напора на внезапное расширение горизонтального потока (см. рис. 6.1, а)

Если диаметры трубы до и после местного сопротивления одинаковы -скоростные напоры - . Поэтому местные потери напо­ра, как и в случае потерь напора по длине трубопровода постоянного сече­ния, измеряются только разностью показаний пьезометров. Так, потери напо­ра на диафрагме, установленной в трубе постоянного сечения (см.рис. 6.1, б).

.

При этом мерные сечения 1-1 и 2-2 (сечения для установки пьезометров) выбирают с таким расчетом, чтобы в них соблюдались, условия плавно изменяющегося движения и транзитная струя полностью заполняла трубу.

Следует заметить, что для белее точного определения местных потерь, из вышеуказанных выражений нужно вычесть потери по длине на участке с местным сопротивлением. Однако, ввиду малости длины рассматриваемого участка и значений потерь напора по длине, ими обычно пренебрегают.

В инженерных расчетах для определения потерь механической энер­гий на местных сопротивлениях используется формула Ю. Вейсбаха, выра­жающая потери в долях от скоростного напора

(6.1)

где - коэффициентместных потерь сопротивления;

V - средняя скорость потока за местным сопротивлением.

В большинстве случаев при подсчете местных потерь напора по фор­муле (6.1) используются в основном справочные эмпирические значения , которые зависят от геометрии местных сопротивлений и числа Re. Теоретические формулы для определения потерь напора получены только для про­стейших видов местных сопротивлений. Так, принятосчитать, что потери напора в случае внезапного расширения трубопровода при Re > 3000 с доста­точным приближением выражаются теоретической формулой Ж. Борда.

(6.2)

где - средние скорости движения до и после расширения. Из формулы (6.2) следует, что потерн напора вследствие внезапного расширения рав­ны скоростному напору потерянной скорости. Эта формула с помощью уравнения неразрывности можст быть приведена к виду формулы (6.1), откуда следует, что

(6.3)

При внезапном сужении канала (диафрагма в трубе, резкое уменьше­ние диаметра грубы) струя жидкости, пройдя отверстие площадью , сжи­мается и достигает наименьшей площади 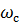в сечении С-С (см. рис. 6.1, б, в). Затем струя постепенно расширяется, пока площадь ее сечения не станет равна площади сечения трубы ₂. При турбулентном движении местные по­тери при этом равны потерям напора на участке расширения струи. Поэтому коэффициенты рассматриваемых местных сопротивлений определяются по формуле (6.3). где вместо подставляется значение ₀ определяемое из формулы А.Д. Альтшуля.

(6.4)

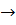
При входе в трубу из резервуара, являющимся частным случаем вне­запного сужения, коэффициент сопротивления входа при острых кромках =0,4 - 0,5, что соответствует значению коэффициента, определенного из формул (6.4) и (6.3) при 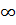. При закругленных кромках = 0,2 и при весьма плавном входе = 0,05. Эти значения коэффициентов указаны для турбулентного режима движения жидкости, который присутствует в ме­стных сопротивлениях в подавляющем большинстве случаев. При этом зна­чения коэффициентов приобретают постоянные значения, не зависящие от числа Re.