Общие сведения. Опыт, проведенный Рейнольдсом, показывает, что при движении жидкости можно различать два режима - ламинарный и турбулентный

Опыт, проведенный Рейнольдсом, показывает, что при движении жидкости можно различать два режима - ламинарный и турбулентный. При ламинарном режиме жидкость движется слоями, скользящими относительно друг друга без перемешивания. Изменение скорости возможно только вдоль пути перемещения частиц. Такая вариация скорости называется продольными пульсациями.

При турбулентном режиме движение жидкости неупорядоченное, ее частицы имеют сложную, все время меняющуюся траекторию. Кроме продольного перемещения появляются поперечные перемещения, которые представляют собой поперечные пульсации.

Потери энергии при движении жидкости существенно зависят от режима. Для трубопровода круглого сечения потеря напора может быть выражена в общем виде:

, (3.1)

где k - коэффициент пропорциональности;

m - степенной коэффициент, определяющий соотношение скорости и величины потерь.

При ламинарном режиме m»1, при турбулентном изменяется от 1 до бесконечности.

Характеристикой режимов движения является безразмерный критерий Рейнольдса, который для напорного движения в круглых трубах определяется по формуле:

, (3.2)

где 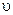- средняя скорость движения потока жидкости, м/с;

d - внутренний диаметр, м;

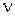- коэффициент кинематической вязкости, м²/с (приложение 1).

При значении числа Рейнольдса, равным примерно 2320 происходит переход ламинарного режима в турбулентный и наоборот турбулентного режима в ламинарный. Следовательно при R_e<2320 режим движения жидкости будет ламинарным, а при R_e>2320- турбулентным. Число R_e=2320 называют критическим, а соответствующую этому числу скорость движения жидкости- критической.