Обработка опытных данных. 5.1. Определить расход воды (м3/с) по формуле:

5.1. Определить расход воды (м³/с) по формуле:

, (3.3)

где m- масса воды, кг;

- удельный вес воды, Н/м³; ( =9810 Н/м³);

t- время замера, с.

5.2. Найти среднюю скорость движения воды в трубопроводе:

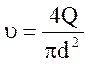, (3.4)

где d - внутренний диаметр трубки, м. d=0,025м.

5.3 Определить потери напора, м: 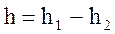(3.5)

5.4 Подсчитать для каждого из исследованных режимов значение числа Рейнольдса по формуле 3.2.

5.5 Для определения критической скорости и критического числа Рейнольдса строят логарифмическую анаморфозу.

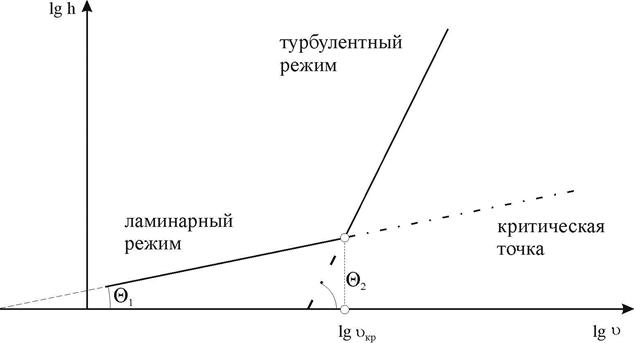
Рис. 3.2. Логарифмическая анаморфоза

Для этого значения h (мм) и 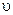(м/с) логарифмируют и откладывают по осям ординат и абсцисс соответственно, получая систему опытных точек, по которым возможно провести две пересекающиеся прямые, расположенные к оси абсцисс под разными углами и .

Прямая имеющая угол наклона соответствует ламинарному режиму движения, а прямая с углом наклона соответствует турбулентному режиму.

Из графика логарифмической анаморфозы определяют точку пересечения прямых, которая является логарифмом критической скорости. Далее находят значение этой точки (путем потенцирования) и по ней вычисляют критическую скорость:

(3.6)

Полученную величину подставляют в формулу 3.2 и определяют критическое число Рейнольдса. Опытное значение сравнивают с теоретическим и делают вывод.

Тангенсы углов и выражают особый показатель степени m₁=tg при ламинарном режиме движения и m₂=tg при турбулентном.

Полученные опытные величины показателей сравнить с существующими m₁ и m₂.