Общие указания. Задача об истечении жидкости через отверстия одна из основных в гидравлике и сводится к определению скорости истечения и расхода вытекающей жидкости

Задача об истечении жидкости через отверстия одна из основных в гидравлике и сводится к определению скорости истечения и расхода вытекающей жидкости. В зависимости от размеров и формы различают малые и большие отверстия в тонкой и толстой стенках, в зависимости от расположения отверстия и условий протекания жидкости различают совершенное и несовершенное, полное и неполное сжатие струи, истечение из затопленного и незатопленного отверстия при постоянном и переменном напоре. Малым отверстием называется такое отверстие, диаметр которого меньше 0,1Н (Н— действующий напор). Стенка считается тонкой, когда ее толщина меньше трех диаметров отверстия ( <3d).

Рассмотрим истечение жидкости через малое незатопленное отверстие в тонкой стенке. Для определения скорости истечения и расхода жидкости составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, проходящего через центр отверстия и сжатого сечения струи (рис.4.1.)

Рис. 4.1.

В данном случае Z₁=H, а Z₂=0. Полагая, что площадь поверхности жидкости в сечении 1-1 W > 200×w, можно считать . Тогда уравнение примет вид:

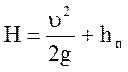
Потери напора в данном случае представляют собой местные потери на входе в отверстие, т.е.:

Решая уравнение Бернулли относительно скорости истечения u, получим:

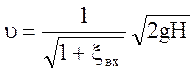
Обозначив окончательно находим скорость истечения жидкости из отверстия в тонкой стенке:

,

где j - коэффициент скорости.

Расход жидкости в сжатом сечении можно определить из уравнения неразрывности потока:

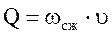
Но практически удобнее пользоваться вместо площадью отверстия w, между которыми есть связь (e - коэффициент сжатия). Обозначив получим:

,

где m - коэффициент расхода.