Сила давления жидкости на криволинейные поверхности. Определение давления жидкости на цилиндрическую поверхность представляет собой частный случай общей задачи о давлении жидкости на криволинейные поверхности

Определение давления жидкости на цилиндрическую поверхность представляет собой частный случай общей задачи о давлении жидкости на криволинейные поверхности. Чтобы получить общее решение, возьмём сосуд произвольной формы и выделим его на стенке какую-либо произвольную поверхность S, ограниченную контуром AMBN. Будем искать составляющие полного давления на эту поверхность по координатным осям, выбрав, например, начало координат на свободной поверхности жидкости и расположив оси так, как это показано на чертеже. При этом ограничимся определением лишь одной составляющей R_x. Параллельной оси x, поскольку остальные составляющие можно найти аналогичным образом. Найдём проекцию поверхности S на некоторую плоскость NN, нормальную к оси x и расположенную между этой поверхностью и координатной плоскостью ZOY. Отметим, что указанную плоскость проекции NN, как и направление самой оси x, можно выбирать по-разному. На жидкость, заключённую в объёме между поверхностью S, плоскостью NN и поверхностью проектирующего цилиндра, образующие которого параллельны оси x, действуют следующие силы: тяжести (вес) G_x выделенного объёма жидкости; давления жидкости R_Fx на проекцию поверхности S на плоскость NN; давления на боковую поверхность указанного объема (их проекция на ось x равна нулю); реакции R со стороны поверхности S, равная по значению, но обратная по направлению искомой силе давления жидкости. Проектируя эти силы на ось x, имеем:

(2.64)

откуда для проекции силы реакции получаем

(2.65)

Аналогично находят выражения для проекции силы реакции и на другие координатные оси:

	(2.66)
	(2.67)

где - углы между направлением линии действия силы тяжести и осями координат x, y, z.

Таким образом, получаем следующую общую теорему о давлении жидкости на криволинейную поверхность: проекция силы давления жидкости на криволинейную поверхность S на заданную ось x равна сумме проекций на эту ось веса жидкости, находящейся между поверхностью S, поверхностью проектирующего цилиндра и плоскостью проекций, нормальной к оси x, и силы давления жидкости на проекцию поверхности S на ту же плоскость проекции. Силу гидростатического давления на криволинейную поверхность определяют по формуле:

,

(2.68)

где - составляющие силы избыточного давления по соответствующим координатным осям. В случае цилиндрической криволинейной поверхности:

,

(2.69)

где P_x и P_y - горизонтальная и вертикальная составляющие силы P. Горизонтальная составляющая избыточного давления P_x равна силе давления на вертикальную проекцию криволинейной поверхности:

,

(2.70)

где p_m- манометрическое давление на поверхности жидкости; h_c - глубина погружения центра тяжести вертикальной проекции криволинейной поверхности; w_z - площадь вертикальной проекции криволинейной поверхности. Если манометрическое давление на свободной поверхности жидкости равно нулю (p₀ = p_ат), то

.

(2.71)

Вертикальная составляющая P_z равна весу жидкости в объёме тела давления. Тело давления расположено между вертикальными плоскостями, проходящими через крайние образующие цилиндрической поверхности, самой цилиндрической поверхностью и свободной поверхностью жидкости или её продолжением. (рисуно 2.8)

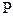
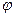
Рисунок 2.8 -

Если давление на свободной поверхности жидкости p₀ ¹ p_ат, то тело давления ограничивается сверху пьезометрической плоскостью, удалённой от свободной поверхности жидкости на расстояние Направление силы P определяется тангенсом угла j:

.

(2.72)

Если криволинейная поверхность не цилиндрическая, то горизонтальную составляющую P_y определяют аналогично P_x..