
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гидравлические элементы живого сечения потока в канале.
Наиболее часто встречаются поперечные сечения каналов, показанные на рисунок рисунке 7.2. Приведем ниже формулы, служащие для определения величин ω, χ и R.
Симметричное трапецеидальное поперечное сечение (рисунок 2а).Здесь b – ширина канала по дну; h – глубина наполнения канала; величина m, указанная на чертеже – коэффициент откоса:
m=ctg ψ
где угол ψ (см. чертеж) задают не по соображениям гидравлического расчета, а учитывая устойчивость грунта откоса (если откосы канала образуются нескальным грунтом). Ширина потока поверху:
B=b+2mh
Величины живого сечения ω и смоченного периметра χ удобно вычислять по следующим геометрическим зависимостям:

Зная ω и χ, определяем величину R
R=ω/χ
Иногда при расчете каналов пользуются понятием относительной ширины канала по дну:
Β = b ⁄ h
 Рисунок 7.2 - Виды безнапорных русел
Рисунок 7.2 - Виды безнапорных русел
|
Величины ω и χ через β выражаются следующим образом:
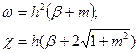
Прямоугольное поперечное сечение (рисунок 2 б)
Здесь B = b; m = ctg 90˚=0
W = =bh; χ = =b + 2h
в случае весьма широкого прямоугольного русла χ ≈ b. 
 Рисунок 7.3 -
Рисунок 7.3 -
|
Треугольное поперечное сечение ( рис.2в)
Здесь b = 0; B = 2mh;
W = mh2 ; 
Параболическое поперечное сечение (рисунок 7.2 г)
Уравнение параболы, образующей смоченный периметр, имеет вид:

Где р – параметр параболы: оси x и y указаны на рис 2г. Для такого русла ширина потока поверху В может быть найдена (для заданной глубины h) из уравнения:


| При (h:B) ≤ 0,15; При (h:B) ≤ 0,33 При 0,33 < (h:B) < 2,00 При 2,00 ≤ (h:B). |
Дата добавления: 2015-04-18; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |