Примеры и задачи. Насос перекачивает мазут по всасывающей линии трубопровода длиной ℓ, диаметром d и шероховатостью поверхности трубы 0,1 мм

Пример 5.1.

Насос перекачивает мазут по всасывающей линии трубопровода длиной ℓ, диаметром d и шероховатостью поверхности трубы 0,1 мм. Уровень жидкости в баке H, показание вакуума на входе в насос p_v, а ртутного манометра h_рт, коэффициент местных сопротивлений x_м = 2,5.

Рассчитать расход Q.

Дано: вязкость 75 мПа∙с, плотность 890 кг/м³, ℓ = 7 м,d = 150 мм, H = 4 м,p_v = 50 кПа, h_рт =100 мм.

Решение:

Если жидкость несжимаемая, то силы инерции учитываются инерционным напором. Тогда для горизонтального трубопровода Ź1=Ź2, постоянного диаметра v1=v2, после выключения насоса р1=р2=ра, уравнение Бернулли для

Пример 5.2.

Центральный насос перекачивает нефть с кинематическим коэффициентом вязкости 3,5*10^-5 м²/с по горизонтальному трубопроводу длиной 100м, диаметром 200мм и расходом 10 л/с. После выключения центробежного насоса давления на входе в насос и на выходе из трубопровода упало до атмосферного. Потерями напора в насосе и сжимаемостью нефти пренебречь. Найти закон изменения скорости жидкости в трубопроводе.

Решение :

Если жидкость несжимаемая, то силы инерции учитываются инерционным напором. Тогда для горизонтального трубопровода Ź1=Ź2, постоянного диаметра v1=v2, после выключения насоса р1=р2=ра, уравнение Бернулли для нестационарного движения запишется :

hτ +hi=0

Так как режим движения ламинарный:

Re= v*d = 4Q = 4 * 10^-2 =1.81· 10³ <Reкр=2000

υ πdυ 3.14 * 0.2 * 3.5 * 10 ^-3

потери напора на трение определяются по формуле(5.9):

hτ=128lυQ = 32lυ v,

πd⁴g d²g

а инерционный напор по формуле (10.7),тогда :

32 l υ v + l ∂ v = 0

d²g g ∂ t

Интегрируя это выражение при условии

t=0; v=vo= 4Q = 4 * 10 =0.318 м/с

πd² 3.14 * (0.2)²

получаем v=vo l^-32υt/d =0.318 * l^-0.028t м/с

Пример 5.3.

Найти потери давления при движении воздуха в вентиляционном канале , при температуре Расход воздуха при заданных условиях

Решение:

Заданному состоянию воздуха соответствует кинематический коэффициент вязкости и плотность

Находим число Рейнольдса, характеризующее поток воздуха в канале:

Определим относительную шероховатость канала (при абсолютной эквивалентной шероховатости ):

Находим величину коэффициента гидравлического трения по обобщенной формуле

Определяем потерю полного давления на 1 пог. м канала:

Задача 5.1

При мгновенном закрытии задвижки давление в трубопроводе повышается на величину Δp. Как изменится повышение давления, если время закрытия задвижки составляет 1 с, 2 с, 3 с, 4 с. Длина трубопровода 1,2 км, а скорость звука в нем 1200 м/с.

Ответ. Не изменится; не изменится; уменьшается в 1,5 раза, в 2 раза.

Задача 5.2

По стальному трубопроводу длиной 1,5 км, диаметром 200 мм и толщиной стенок 6 мм перекачивается нефть плотностью 830 кг/м³ и модулем упругости 1,15 * 10⁹ н/м². Модуль упругости стали считать в 300 раз больше модуля упругости нефти. Определить скорость распространения гидравлического удара в трубопроводе и повышение давления в нем, если за время 5 с скорость нефти в трубопроводе уменьшилась на 1 м/с.

Ответ . 1120 м/с; Δp=0,498 10⁶ Па

Задача 5.3

Клапан поршневого насоса, подающего жидкость в напорный трубопровод длиной 100м, диаметром 150 мм, срабатывает при расходе жидкости 1,5 10^-3 м3/с. Определить изменение давления после клапана в напорной магистрали, если клапан закрылся за 0,1 с. Скорость распространения гидравлического удара 1200 м/с, а плотность жидкости 1000 кг/м³ .

Ответ : Δp=-1.02 10⁵ Па

Задача 5.4

По трубопроводу длиной 3 км перекачивается жидкость со средней скоростью 3 м/с. На расстоянии 1км от входа в трубопровод находится задвижка, которая закрывается в течение 2-х секунд. Найти перепад давления на задвижке после ее закрытия, если скорость распространения гидравлического удара равна с=1300 м/с, а плотность жидкости 860 кг/м³.

Ответ: Δp=5,93 10⁶ Па

Задача 5.5

При включении насоса расход жидкости меняется по линейному закону и за время to=5 с возрастает от нуля до 10^-2 м3/с. Определить давление , которое должен создавать насос в любой момент времени 0<t<to для обеспечения заданного закона изменения подачи, если перекачивается жидкость плотностью 10³ кг/м³ по горизонтальному трубопроводу длиной 5 км, диаметром 100 мм. Скорость распространения гидравлического удара равна 1400м/с. Потери напора не учитывать.

Ответ: Δp=0,356 10⁵ t Па

Задача 5.6

По горизонтальному трубопроводу длиной 1 км, диаметром 200 мм центробежный насос перекачивает несжимаемую жидкость со средней скоростью vо=2 м/с. Определить закон изменения скорости жидкости со временем и скорость жидкости в момент времени t=5 с после остановки насоса. Коэффициент гидравлического сопротивления принять равным λ=0,02, а движение считать турбулентным.

Указание. При остановке насоса давление считать равным атмосферному.

Ответ: v=1.33 м/с v= v_o

(1+λv_o/2d*t)

Задача 5.7

Определить потери напора в газопроводе низкого давления, транспортирующем газ пр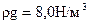и и диаметр газопровода Расход газа Длина участка l= м.

Задача 5.8

Определить потери давления в газопроводе высокого давления диаметром по которому транспортируется газ и Абсолютное давление газа в начале участка расход газа Длина участка газопровода