Уравнение простого трубопровода

Рассмотрим вывод уравнения простого трубопровода для схемы короткого трубопровода показанного на рисунке 5.1. Насос из открытого бака перекачивает жидкость в сеть. На входе в насос стоит вакуумметр. Заданы свойства жидкости, материал трубопровода и геометрия трубопровода.

Рисунок 5.1 - Схема короткого трубопровода– Короткий трубопровод: а - истечение под уровень; б – истечение в атмосферу

Для вывода уравнения простого трубопровода в данном случае:

1.5.1.1. Выберем два поперечных сечения там, где известны давления. Нумеруем эти сечения по направлению движения жидкости 1-1 и 2-2. Выбираем плоскость сравнения 0-0 проходящую через центр тяжести нижнего поперечного сечения.

1.5.1.2.Распишем значения z и p в этих поперечных сечениях. Для Рисунок 5.1 z₁ = 0, z₂ = H_гвв, абсолютное давление в первом сечении равно атмосферному давлению p₁ = p_ат, абсолютное давление во втором сечении равно p₂ = p_ат - p_v.

1.5.1.3.Распишем скорости в поперечных сечениях. Площадь первого поперечного сечения гораздо больше площади поперечного сечения трубы, поэтому скорость в первом поперечном сечении гораздо меньше скорости в трубе и примем её равной нулю v₁ = 0. Площадь второго поперечного сечения равна площади поперечного сечения трубы, поэтому скорость во втором поперечном сечении равна скорости в трубе v₁ = v. Подставим полученные значения в уравнении Бернулли для потока реальной жидкости:

.

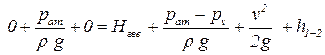(5.1)

Упрощая полученное уравнение, получим

.

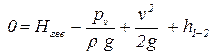(5.2)

1.5.1.4. Находим потери напора в трубопроводе. Потери напора равны сумме потерь напора на местные сопротивления и сумме потерь напора на трение. Местными потерями являются: потери напора на сетке с обратным клапаном, которая ставится на входе в трубу: поворот трубы на 90°; задвижка на трубе. Все эти потери рассчитываются по скорости после местного сопротивления, а это скорость в трубе. По справочникам находим значения коэффициентов этих местных сопротивлений z_сетка, z_пов, z_зад. Потери напора на трение находится по формуле Дарси-Вейсбаха. Тогда потери напора равны

(5.3)

1.5.1.4. Подставим потери напора в уравнение Бернулли, получим:

(5.4)

Это и есть уравнение простого трубопровода для данного случая. Это уравнение не зависит от типа расчета трубопровода.