КАТЕГОРИИ:

Астрономия Биология География Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Механика Образование Охрана труда Педагогика Политика Право Психология Риторика Социология Спорт Строительство Технология Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Опишите известные Вам критерии направленности процессов и дайте их математическое обоснование. В каком случае удобнее пользоваться каждым из них и почему?

Стр 1 из 4Следующая ⇒

Существует несколько критериев направленности процессов:

1) Энтропия как критерий направленности процессов;

2) Направленность процессов при V и Т =const;

3) Направленность процессов при Р и Т =const;

1) Рассмотрим изолированную систему С_т+СО₂→2СО.

Если реакция протекает в прямом направлении, то процентное содержание СО₂ будет уменьшаться, а СО- увеличиваться. Если же реакция протекает в обратном направлении, то, наоборот, СО₂ будет увеличиваться, а СО- уменьшаться.

Для энтропии dS≥ δQ /T, но т.к. у нас система замкнутая и Q=0, то , следовательно dS≥0.

Для реальных процессов dS>0, следовательно процесс протекает так, чтобы энтропия возрастала.

$$$$ Вставить рис.3 $$$$$ 1) Исходное состояние 1- реакция протекает в прямом направлении; 2) Исходное состояние 2- реакция протекает в обратном направлении; 3) В точке 3- равновесие.

В состоянии равновесия энтропия максимальна.

2) Пусть система не замкнута, т.е. Q≠0. При необратимых процессах dS> δQ /T, учтем, что V=const:

δQ=dU, откуда dU-TdS≤0. Учтем, что T=const:

d(U-TS) ≤0, причем U-TS – свойство, т.к. составлена из свойств системы. Следовательно

F=U-TS –энергия Гельмгольца. dF≤0, dF<0/

Таким образом при постоянных V и Т процессы протекают в таком направлении, чтобы энергия Гельмгольца уменьшалась.

$$$$ Вставить рис.4 $$$$$ 1)В точке 1- реакция протекает в прямом направлении; 2) В точке 2- реакция протекает в обратном направлении; 3) В точке 3- равновесие.

В состоянии равновесия энергия Гельмгольца минимальна.

3) При необратимых процессах dS≥ δQ /T.

Р=const, поэтому δQ_р=dH. Следовательно dH-TdS≤0.

T=const, поэтому d(H-TS)≤0, причем H-TS – свойство, т.к. составлена из свойств системы/ Следовательно G= H-TS – энергия Гиббса, dG≤0, dG<0, т.е ΔG<0.

Таким образом при постоянных Р и Т процессы протекают в таком направлении, чтобы энергия Гиббса уменьшалась.

• Изменение энтропии может служить критерием направленности процессов только в изолированных системах. При обратимых процессах, при постоянных температуре и объеме энергия Гельмгольца не изменяется, а при необратимых- может только убывать. Это означает, что функция F является критерием, который позволяет судить о направлении процессов в незамкнутых системах. Энергия Гиббса может служить критерием направленности процессов только при необратимых процессах (она должна убывать), при обратимых процессах G не изменяется.

Объясните, что характеризует изменение энергии Гиббса системы в изотермическом процессе. Чем оно отличается от изменения свободной, внутренней энергии и энтальпии и почему? (см. лекции Ватолин 38) (20-21) и (35-37) Никольский

Почему внутренняя энергия идеального газа не зависит от давления, а реального - зависит. При высоких или низких давлениях будет сильнее отличаться внутренняя энергия (Н2О)пар от энергии идеального газа при одинаковой температуре? Почему? (20-21) Никольский

Под идеальными (совершенными) газами понимают такие газообразные тела, которые подчиняются следующим трем законам:

закону Джоуля — внутренняя энергия идеального газа зависит только от температуры и не зависит от давления или объема, т. е.:

(dU/dV)_t=0 или U = U(t); (1.17)

законам Бойля — Мариотта и Авогадро.

Два последних закона можно выразить уравнением:

pV = n∙f(t), (1.18)

где п — число моль газа, a f(t)—универсальная функция, зависящая только от температуры и одинаковая для всех идеальных газов.

До сих пор, говоря о температуре, мы не интересовались, по какой шкале и с помощью какого прибора она измеряется, так как для нас важна была только качественная или полуколичественная сторона понятия «температура» (больше, меньше). При изучении свойств совершенных газов мы можем рационально установить строгое количественное понятие о температуре, введя так называемую газовую шкалу температуры. Это можно сделать, приняв за температуру величину, пропорциональную f(t) в уравнении (1.18):

где R — коэффициент пропорциональности, одинаковый для всех идеальных газов независимо от их природы; — температура по газовой шкале.

Уравнение (1.18) теперь примет форму:

(1.19)

Значение коэффициента R зависит от единиц измерения давления, объема и температуры. Для выбора единицы измерения температуры по газовой шкале в качестве основной реперной точки принимают тройную точку воды*, которой присваивают температуру 273,16 К (0°С).

· Температурой тройной точки воды называют температуру сосуществования жидкой воды, льда и насыщенного водяного пара при отсутствии других газов

Свойства идеальных газов, выраженные уравнениями (1.17) и (1.19) позволяют найти их энергию и энтальпию в зависимости от температуры. Из уравнений (I. 13) и (1.17) следует, что теплоемкости идеального газа (и ) могут зависеть только от температуры. Мы примем, что теплоемкость не зависит и от температуры (что с большой точностью экспериментально подтверждается для одноатомных газов). Тогда из уравнения (1.13) получим, пользуясь газовой шкалой температуры:

(1.20)

где U₀ — константа интегрирования; — молярная теплоемкость газа.

Величина представляет собой значение внутренней энергии идеального газа при θ = 0.

Энтальпия газа, согласно уравнениям (1.6) и (1.20) равна:

H = +pV + (1.20а)

Дифференцируя (1.20а) по θ, получим выражение dH/θ = nR + C_V, сравнение которого с (1.12) дает: C_P = C_V + nR или для 1 моль газа:

= + R. (1.21)

Таким образом, теплоемкость 1 моль идеального газа при р = const всегда на R единиц больше, чем при V = const.

Теперь уравнение для энтальпии идеального газа можно написать так:

H = = (I. 22)

Следовательно, как внутренняя энергия идеального газа, так и его энтальпия линейно зависят от температуры (в газовой шкале), возрастая соответственно на величины 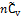или при повышении температуры на 1 градус.

Следует помнить, что всякий реальный газ по мере увеличения его объема при р = const все больше приближается по своим свойствам к идеальному газу, чем и обусловлено большое значение для химической термодинамики изучения свойств совершенных газов.

Что такое химическое сродство? Что принято за меру сродства и почему? У какого металла, хрома или марганца, при комнатной температуре выше сродство к кислороду и насколько? (68-75) Шварцман (200-203) Попель (42-44) Никольский

Химическим сродством называют способность веществ вступать в химическое взаимодействие. Изменение энергии Гиббса используют для определения меры химического сродства веществ. Константа равновесия К_р характеризует степень протекания реакции в ту или иную сторону. Поскольку ΔG⁰= ΔH⁰-TΔS⁰ и ΔG⁰=-RTln К_р, то -RTln К_р= ΔH⁰-TΔS⁰, откуда Rln К_р= ΔS⁰- ΔH⁰/T. Отсюда видно, что чем больше величина ΔS⁰ и чем меньше ΔH⁰/T, тем полнее идет реакция. Из уравнения видно также, что чем выше температура, тем большее значение имеет величина ΔS⁰ (энтропийный фактор) и меньшее ΔH⁰/T (энтальпийный фактор).

Cродством металла к кислороду называют стандартное изменение энергии Гиббса реакции образования оксида, взятое с обратным знаком. Обычно при анализе реальных процессов обсуждается не упругость диссоциации оксида (давление кислорода p_O₂ при равновесии системы кислород- оксид), а окислительный потенциал системы –ΔG⁰.

Используя справочные данные, найдем –ΔG⁰ для реакций:

4Cr+3O₂=2Cr₂O₃ и 2Mn+O₂=2MnO при комнатной температуре (25⁰С или 298 К)

Вещества	ΔH₂₉₈⁰, Дж/моль	ΔS₂₉₈⁰, Дж/моль
O₂		205,04
Cr		23,64
Cr₂O₃	-1140560	81,17
Mn		32,01
MnO	-385100	61,5

ΔG₂₉₈ ⁰= ΔH₂₉₈⁰-Т ΔS₂₉₈⁰, откуда ΔH₂₉₈⁰=(∑ν_i* ΔH₂₉₈⁰⁽ⁱ⁾)_{прод. р-ии}-(∑ν_i* ΔH₂₉₈⁰⁽ⁱ⁾)_{исх в-ва.}, а

ΔS₂₉₈⁰=(∑ν_i* ΔS₂₉₈⁰⁽ⁱ⁾)_{прод. р-ии}-(∑ν_i* ΔS₂₉₈⁰⁽ⁱ⁾)_{исх в-ва} (где ν_i- стехиометрический коэффициент для i-го реагента).

Таким образом, для реакции 4Cr+3O₂=2Cr₂O₃ : ΔH₂₉₈⁰= -2281120 Дж/моль, ΔS₂₉₈⁰= -547,34 Дж/моль, откуда ΔG₂₉₈ ⁰= -2118012,68 Дж/моль.

Для реакции 2Mn+O₂=2MnO : ΔH₂₉₈⁰=-770200 Дж/моль, ΔS₂₉₈⁰=-146,06 Дж/моль, откуда ΔG₂₉₈ ⁰= -726674,12 Дж/моль.

У хрома -ΔG₂₉₈ ⁰ больше, чем у марганца: 2118012,68 Дж/моль - 726674,12 Дж/моль=1391,338 кДж/моль.

Таким образом, у хрома при комнатной температуре сродство к кислороду больше, чем у марганца на 1391,338 кДж/моль.

8. Что такое константа равновесия? От каких параметров она зависит? Как, используя константу, определить смещение равновесия реакции С_гр+СО₂=2 СО с повышением температуры, давления и дисперсности графита? (см. лекции Ватолин 38)
(366-370) Никольский

• Рассмотрим реакцию А+2В=С при постоянном давлении и температуре.

Изменение энергии Гиббса для этой реакции ΔG=[Дж/мольА]=G_C-G_A-2G_B (1).

Проведем ту же реакцию в стандартных условиях при той же температуре:

ΔG⁰=G_C⁰ -G_A⁰-2G_B⁰ (2).

Вычтем из (1) (2), (1)-(2)=(3)

ΔG -ΔG⁰= G_С-G_C⁰ –(G_А- G_A⁰)-2(G_В-G_B⁰),

причем G_С-G_C⁰=RTlna_C, G_A-G_A⁰=RTlna_A, G_B-G_B⁰=RTlna_B, откуда следует ΔG -ΔG⁰=RTln(a_C/a_A_*a_B²) (3)

Запишем уравнение (3) для состояния равновесия реального процесса, т.е. ΔG=0:

- ΔG⁰ =RTln(a_C/a_A_*a_B²)_равн, где a_C, a_A_,a_B² – активности веществ А, В и С для состояния равновесия.

Таким образом, активности реагирующих компонентов связаны между собой определенным соотношением, которое является выражением закона действующих масс. При равновесии такая дробь, числитель которой есть произведение активностей образующихся при реакции веществ, а знаменатель- произведение активностей исходных веществ, есть величина постоянная и называется константой равновесия К_а:

К_а= a_C/a_A_*a_B²

Показателями степеней при активностях являются стехиометрические коэффициенты, в которых данные вещества вступают в реакцию.

Константа равновесия зависит от температуры и природы реакции и не зависит от давления и концентрации реагентов.

• Смещение равновесия реакции можно определить, используя принцип Ле-Шателье, согласно которому: если на систему, находящуюся в равновесии оказать внешнее воздействие, то равновесие сместится т.о., чтобы уменьшить внешнее воздействие. Однако, используя константу равновесия, можно также определить смещение равновесия реакции С_гр+СО₂=2СО с повышением температуры, давления и дисперсности графита.

Запишем константу равновесия для реакции С_гр+СО₂=2СО:

К_а= (a_C_О² /a_С*a_СО2)_равн, т.к а_С=1(графит), то можно записать для газов: К_а=(Р_СО²/Р_СО2)_равн.

Т.к. Р_СО=Р*(%СО/100) и Р_СО2=Р*(%СО₂/100), то К_а=Р*%СО²/(100*%СО₂)_равн.

Согласно уравнению изобары химической реакции (∂lnK_a/∂T)_P=ΔH⁰/RT² с увеличением температуры константа равновесия должна возрастать, следовательно (%СО)↑ , а (%СО₂)↓. Таким образом, с увеличением температуры равновесие реакции сместится вправо (в сторону увеличения %СО и уменьшения %СО₂).

Рассмотрим случай, когда давление повышается (Т=const). Константа равновесия при этом останется прежней (К_а≠ f(P)), тогда (%СО)↓, а (%СО₂)↑, так чтобы К_а была прежней. Таким образом, с увеличением давления равновесие реакции сместится влево (в сторону увеличения %СО₂ и уменьшения %СО).

Влияние дисперсности?????????????????

9. Что такое активность и коэффициент активности? Для чего введены эти характеристики и какие способы их количественного определения Вы знаете? В каких случаях каким экспериментальным способом лучше воспользоваться для их определения и почему?
(см. лекции Ватолин 36)

• Термодинамическая активность i-го вещества (а_i)- это отношение фугитивности (для решения задач химического равновесия давление заменяют летучестью или фугитивностью f_i при его высоких значениях) вещества в реальном состоянии к фугитивности в стандартном состоянии при постоянной температуре.

a_i=f_i/f_i⁰(1),(G_i=G_i⁰+RTlna_i G_i⁰-для чистого вещества)

Активность также определяется как отношение парциального давления i-го компонента над раствором к парциальному давлению чистого компонента:

a_i=P_i/P_i⁰ (2),

Активность удовлетворяет следующим требованиям:

1) Через нее просто выражаются все термодинамические свойства растворов;

2) По величине а можно предполагать возможный переход компонента из одной фазы в другую;

3) В предельных случаях (для ид. р-ров) она совпадает с концентрацией, а в реальных растворах показывает степень отклонения от идеальности;

4) С ее помощью сохраняется форма уравнений, выражающих законы идеальных растворов.

• Из уравнения (2) и закона Рауля (x_i= P_i/P_i⁰ ) следует, что для совершенного раствора активность равна молярной доле. Если поведение раствора отклоняется от совершенного, то a_i≠x_i. Степень этого отклонения определяется величиной коэффициента активности:

γ_i=a_i/x_i, в случае совершенных растворов γ_i=1 и a_i=x_i. Для реальных растворов коэффициент активности может быть как меньше 1 (отрицательные отклонения), так и больше (положительные отклонения). Если для реальных растворов вместо молярной доли использовать активность, то закон Рауля сохраняет свою форму, т.е. P_i=P_i⁰a_i.

Из сказанного следует, что введение коэффициента активности является формальным приемом, упрощающим термодинамические соотношения и позволяющим проводить расчеты равновесий с участием реальных растворов.

• Существует несколько способов определения количественного определения активности и коэффициента активности.

1) Определение активности по равновесию раствора с газовой фазой.

Расплав выдерживается при заданной температуре под газовой фазой до наступления равновесия. Газовая фаза должна содержать элемент, активность которого мы определяем в расплаве. По равновесному составу расплава и газовой фазы определяют активность компонента в расплаве.

Этот метод применим для металлических и оксидных расплавов. С его помощью были определены активности и коэффициенты активности углерода, серы, кислорода в металлических расплавах.

2) Определение активности по упругости пара.

- Статические (равновесные) методы определения упругости пара.

Здесь используются метод прямого определения Р_нас (Р_исх=10^-6-10^-8), который применим для Р_нас>0,1мм рт. ст. (высокая упругость пара, легко испаряется).

Также применяется метод измерения убыли веса вещества. При высокой температуре происходит испарение расплава и вес тигля уменьшается. Р_насV=ΔPRT/gM , где ΔP- изменение веса, g- ускорение свободного падения. Метод используется для веществ с большим Р_нас.

Вообще статические методы применимы для расплавов , компоненты которых обладают различной упругостью пара. Например для Fe-Mn : Р_Fe^нас<<Р_Mn^нас, а для Fe-Ni нельзя использовать этот метод.

- Динамические методы:

Метод Лангмюра основан на определении скорости сублимации (разгонка) или испарения в вакууме с открытой поверхности при заданной температуре. Предполагается, что испарение протекает в диффузионном режиме. Метод применим для Р_нас <10^-6мм рт. ст. P_нас=2279,6G(T/M)^1/2/Sτ, где G- количество испарившегося Ме, г.; S- площадь испарения, см²; τ-время испарения, с; V-скорость испарения; Т- температура, К; М- атомная масса пара, г/моль. Предполагается, что все атомы, достигая мишень. Конденсируются на ней.

Эффузионный метод (метод Кнудсена). Чтобы уменьшить ошибку, связанную с тем, что не все молекулы конденсируются на мишени, упругость пара измеряют по скорости его истечения в высоком вакууме через калибровочное отверстие. Р_нас=10^-1-10^-8мм рт.ст. В печи создается вакуум. В ходе опыта определяется изменение веса тигля или инертной пластины: Р_нас=2279,6G(T/M)^1/2/SτK, где К=f(d,l)-определяется по эталонному расплаву.

Метод несущего газа можно применять для расплавов, компоненты которого имеют одинаковую упругость пара (Fe-Ni). Над поверхностью расплава пропускают нейтронный газ, уносящий пары компонентов. Пар конленсируется в зоне конденсации, затем снимают конденсат и проводят его химический анализ. Р_нас=10-10^-2мм рт.ст. Р_нас=Р_об*n_i/n_i+n_j+n_газ, где n_i, n_j- число молей компонентов расплава в конденсате (определяется химическим путем), n_газ- число молей , пропущенного через систему газа.

3) Определение активности по распределению элемента между двумя фазами.

Метод основан на том, что в состоянии равновесия активности одного и того же вещества находятся в разных фазах.

a_i¹=a_i², например Ag/Fe-Mn => Ag-Mn/Fe-Mn , Один из растворов должен быть близок к идеальному (Fe-Mn- идеальный раствор), т.е. a_Mn^Ag=a_Mn^Fe, а Ag-Mn- б.р.р. Итого f_Mn^Fe^-^Mn^-^C=f_Mn^Ag[Mn]^Ag/[Mn]^Fe^-^Mn^-^C.

4) Определение активности методом ЭДС.

Методы ЭДС позволяют получать точные значения активности компонентов металла и шлака, вести автоматическую регистрацию записи. Величину ЭДС необходимо измерять компенсационным способом, т.е. тогда, когда через цепь ток не протекает, а величина ЭДС принимает максимальные значения, потому что отсутствует напряжение на другом участке цепи.

Что такое парциально-молярные величины в растворах? Для чего они введены? Как по известной зависимости молярной энергии Гиббса от состава раствора найти отличие химического потенциала любого компонента от стандартного значения? (см. лекции Ватолин 44) (98-105) Шварцман

Чтобы установить зависимость равновесных свойств растворов от состава и свойств компонентов, пользуются парциальными молярными величинами.

Рассмотрим какое-нибудь экстенсивное (зависящее от количества раствора) термодинамическое свойство g раствора. К экстенсивным термодинамическим свойствам относятся объем, внутренняя энергия, энтропия, энтальпия, теплоемкость, энергия Гиббса и др.

Для двухкомпонентного раствора, состоящего из растворителя и растворенного вещества, его экстенсивное свойство зависит от числа молей n₁ растворителя, числа молей n₂ растворенного вещества, давления p и температуры Т:

Учитывая, что экстенсивное свойство g раствора является функцией состояния, возьмем полный дифференциал от этого выражения при постоянстве р и Т:

(1)

Обозначим

(2)

Тогда

(3)

где - парциальная молярная величина или свойство i-го компонента в растворе. Парциальной молярной величиной i-го компонента раствора называется изменение данного экстенсивного свойства раствора при добавлении 1 моля i-го компонента к большому количеству раствора при постоянстве давления, температуры и числа молей остальных компонентов. Большое количество раствора указывается для того, чтобы добавление одного моля i-го компонента практически не изменяло состав раствора. Для чистого вещества парциальная молярная величина равна свойству чистого вещества:

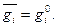(4)

Величину экстенсивного свойства g раствора находим, проинтегрировав уравнение (3):

(5)

Постоянная интегрирования в уравнении (5) равна нулю, так как при всех .

Если в качестве экстенсивного свойства раствора взять, например, объем, то уравнение (5) преобразуется к виду

, (6)

где - общий объем раствора. Аналогично, при постоянстве состава раствора можно через парциальные молярные величины выразить и другие экстенсивные свойства раствора.

Если одновременно изменяются и состав раствора, и его количество, то при дифференцировании (5) получаем общее изменение экстенсивного свойства:

. (7)

Приравняв уравнения (3) и (7), получаем уравнение Гиббса-Дюгема:

. (8)

В общем виде уравнение Гиббса-Дюгема:

, при и (9)

Это уравнение (9) иногда записывают иначе:

, . (10)

Среди парциальных молярных величин особое значение имеет парциальная молярная энергия Гиббса , которая тождественна химическому потенциалу компонента раствора

. (5)

Парциальные молярные величины, характеризующие изменение экстенсивных свойств раствора, могут быть, в отличие от самих свойств, как положительными, так и отрицательными. Они имеют то же значение в термодинамических расчетах процессов в растворах, что и соответствующие функции (U, H, G, S, C_p) при расчетах реакций, протекающих с участием чистых веществ. Например, для чистого вещества известны соотношения:

(6)

Для парциальных молярных величин компонентов раствора справедливы аналогичные термодинамические соотношения:

(7)

Практическое значение парциальных молярных (пм) величин состоит в том, что между ними сохраняются по форме те же термодинамические (тд) соотношения, что и между обычными тд величинами.

Таким образом, при помощи пм величин можно применить к растворам весь математический аппарат химической термодинамики для чистого вещества. Это дает возможность выразить через тд уравнения любые равновесные свойства раствора, к которым относятся давление пара компонентов над раствором, понижение температуры замерзания и повышение температуры кипения раствора, растворимость веществ, распределение вещества между двумя несмешивающимися растворителями и др.

Химические потенциалы компонентов раствора связаны с их активностями соотношением:

(8)

где - стандартный химический потенциал.

Активность компонента в растворе определяется выражением

(9)

где - коэффициент активности i-го компонента; - мольная доля i-го компонента.

В случае совершенных растворов 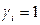и .

В случае БРР для растворителя ; для растворенного вещества

11. Какие модели растворов Вы знаете, и какими уравнениями в каждой из них связан химический потенциал компонента с его мольной долей в растворе? В чём причины отличий химического потенциала компонента реального раствора от модельных? (см. лекции Ватолин 52)

Истинным раствором называется однофазная гомогенная система, образованная не менее чем двумя компонентами. Состав раствора можно изменять непрерывно в определенных пределах. Истинный раствор отличается от коллоидных растворов и механических смесей (суспензии, эмульсии, аэрозоли) тем, что последние представляют собой многокомпонентные гетерогенные системы. Растворы могут быть в трех агрегатных состояниях: газообразном, твердом и жидком.

Различают идеальные, предельно разбавленные и неидеальные растворы.

Идеальные растворы. Идеальным называется раствор, образование которого из компонентов, взятых в одинаковом агрегатном состоянии в любых соотношениях, не сопровождается тепловым эффектом и изменением объема, а изменение энтропии равно изменению энтропии при смешении идеальных газов:

(1)

Тд свойства идеального раствора выражают через парциальные молярные величины. Изменение свойств 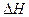, и одного моля раствора связаны с изменениями соответствующих парциальных молярных величин:

(2)

(3)

(4)

где х₁ и х₂ – мольные доли компонентов, из которых состоит раствор (рассматриваются бинарные растворы).

Изменение энтропии при образовании одного моля идеального раствора (энтропия смешения) выражается уравнением

(5)

Из равенств (1) – (5) получаем

(6, 7)

В идеальном растворе энергия взаимодействия различных молекул равна энергии взаимодействия однородных молекул, объемы молекул всех компонентов равны между собой. Таким образом, в идеальном растворе в отличие от идеального газа между молекулами существует взаимодействие.

Физические свойства раствора зависят от его тд свойств. Так как энергия взаимодействия всех молекул в растворе одинакова, то распределение их в пространстве будет равномерным, поэтому изменение энтропии при смешении компонентов идеального раствора не отличается от энтропии смешения идеальных газов. Вследствие этого и тепловой эффект образования идеального раствора из жидких компонентов будет равен нулю. При образовании идеального раствора его объем не меняется, так как объем молекул всех компонентов одинаков.

Растворы, близкие по свойствам к идеальным растворам, существуют в действительности. Они образуются из веществ, близких по своей природе: смеси изотопов, смеси изомеров, смеси органических веществ с разными замещающими функциональными группами и т. п.

Получим соотношение между химическим потенциалом компонента идеального раствора и его составом. Для изменения химического потенциала при образовании раствора можно написать

(8)

Для идеального раствора, учитывая соотношения (6, 7), получаем из уравнения (8)

(9)

(10)

где и 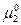- химические потенциалы чистых 1-го и 2-го компонентов раствора. зависит от температуры, давления и природы вещества.

Таким образом, в идеальном растворе для любого компонента i химический потенциал выражается уравнением

(11)

Если компонент – жидкое вещество, то его (дифференциальная) теплота растворения в идеальном растворе равна нулю. Если же компонент – твердое вещество, то его теплота растворения будет равна его теплоте плавления, так как растворение твердого вещества в растворе можно представить процессом, состоящим из двух стадий: плавления твердого тела и растворения полученного жидкого вещества в идеальном растворе. При растворении газообразного вещества в идеальном растворе теплота растворения равна его теплоте конденсации или его теплоте испарения с обратным знаком.

Бесконечно разбавленные растворы (БРР).Бесконечно разбавленным называется раствор, в котором концентрация растворенного вещества бесконечно мала. Бесконечно разбавленный раствор обладает следующими тд свойствами: в любом неидеальном бесконечно разбавленном растворе растворитель подчиняется законам идеальных растворов, а растворенное вещество не подчиняется. Отсюда следует, что в БРР для растворителя можно пользоваться всеми уравнениями, которые справедливы для идеальных растворов.

Если обозначить индексом 1 растворитель, а индексом i (i=2, 3, 4…) растворенное вещество, то разбавленный раствор можно определить как такой, в котором , а . Особенностью такого раствора является то, что молекулы растворенного вещества отделены друг от друга большим числом молекул растворителя. Поэтому имеет место только взаимодействие между растворенным веществом и растворителем, но не между молекулами растворенного вещества. Вследствие этого, если к разбавленному раствору при постоянной температуре добавлять растворитель, то при разбавлении раствора с увеличением его объема не будут изменяться ни энергия U, ни энтальпия Н системы раствор – растворитель:

(12)

подобно тому, как это имеет место в смесях идеальных газов.

Свойства растворителя при переходе в БРР не меняются. А при переходе в БРР i – го вещества, свойства его сильно меняются. Для растворителя будет справедливо следующее выражение для идеального раствора

(13)

Для растворенного вещества будет справедливо

(14)

где - химический потенциал растворенного вещества при концентрации, равной единице, при условии, что раствор сохраняет свойства разбавленного; с₂ – концентрация растворенного вещества.

Неидеальные растворы. Все растворы, которые не подчиняются термодинамическим закономерностям идеальных растворов и БРР, объединяются под общим названием – неидеальные (реальные) растворы.

Равновесные свойства неидеальных растворов определяют термодинамическим путем при помощи эмпирического метода активности, предложенного Льюисом. Химические потенциалы компонентов раствора связаны с их активностями соотношениями:

(14)

где - стандартный химический потенциал.

При вычислении химических потенциалов компонентов раствора выбирают одно из двух стандартных состояний в зависимости от свойств компонентов. Если компоненты взаимно растворимы при любых соотношениях, то за стандартное состояние компонентов выбирают чистые компоненты – первое стандартное состояние. Активность и коэффициент активности в этом состоянии принимают равными единице. Концентрацию компонентов при этом выражают в мольных долях.

Если один из компонентов ограниченно растворим в другом, что часто имеет место при растворении в жидкостях (растворителях) твердых и газообразных веществ, то для растворителя за стандартное состояние принимается чистый растворитель (первое стандартное состояние). За стандартное состояние растворенного вещества принимается гипотетический раствор с концентрацией этого вещества, равной единице, и со свойствами бесконечно разбавленного раствора (второе стандартное состояние). Значение коэффициента активности в этом состоянии принимается равным единице. При этом активность равна концентрации, т. е. тоже единице.

Среди неидеальных растворов выделяют регулярные и атермальные растворы. Регулярные растворы – это реальные растворы, у которых при смешении компонентов, взятых в одинаковом агрегатном состоянии, изменение энтальпии и объема не равны нулю, но изменение энтропии равно энтропии смешения идеальных растворов. Считается, что молекулы раствора расположены абсолютно хаотически, как в идеальных растворах.

Такими свойствами приблизительно обладают растворы неполярных неассоциированных жидкостей, к которым относятся, например, растворы из С₆Н₆ и С₆Н₁₂; С₆Н₁₂ и ССl₄ и др. В этих растворах небольшие различия в энергиях взаимодействия однородных и разнородных молекул не вызывают заметного увеличения числа однородных (или разнородных) молекулярных пар по сравнению со средним статистическим.

Теория регулярных растворов применяется к системам с малыми отклонениями от идеальности.

Атермальные растворы – это реальные растворы, теплота образования которых равна нулю. Близки к атермальным многие растворы высокомолекулярных веществ в обычных низкомолекулярных растворителях. В этих растворах молекулы растворенных веществ в сотни и тысячи раз больше молекул растворителя.

Дата добавления: 2015-04-18; просмотров: 367; Мы поможем в написании вашей работы!; Нарушение авторских прав

12 3 4 Следующая ⇒

lektsii.com - Лекции.Ком - 2014-2024 год. (0.007 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав
Главная страница Случайная страница Контакты