
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Совмещение и экспонирование
Экспонирование и совмещение— операции, обеспечивающие перенос изображения с фотошаблона на пластину, — связаны между собой (рис. 3.10). Для получения точной передачи размеров изображения фотошаблона необходимо одновременно и взаимосвязанно изменять и время экспонирования, и время проявления рисунка. Поскольку одинаково недопустимы как недодержки, так и передержки при экспонировании, оптимальная экспозиция определяется экспериментально. Характер дефектов при неправильно выбранной экспозиции в позитивных и негативных фоторезистах различен.
матических установок требуются специальные опорные знаки в виде непрозрачных штрихов на фотошаблоне и канавок, вытравленных на подложке. Ширина канавок должна быть в 2-4 раза больше ширины штриха.
Вначале с помощью микроскопа / оператор производит грубое совмещение, затем включается фотоэлектрическая система, выполняющая точное совмещение. Размер, форма и контрастность знаков совмещения играют решающую роль в обеспечении точности процесса.
В качестве источников света при экспонировании обычно используют ртутные лампы 2 высокого или сверхвысокого давления мощностью от 100 до 500 Вт, интенсивно излучающие в коротковолновой области спектра, что соответствует полосе максимальной чувствительности большинства фоторезистов (300-450 нм). Это излучение через конденсор 3 попадает на фотошаблон. При контактной фотолитографии разрешающая способность процесса во многом определяется надежностью контакта между экспонируемой пластиной 7 и фотошаблоном 4. За счет зазора 5 между шаблоном и фоторезистом б возникает френелевская дифракция, размывающая контуры изображения. Для уменьшения зазора используют вакуумный или пневматический прижим шаблона к пластине.
В современных прецизионных установках совмещения и экспонирования используются два метода совмещения: визуальный и фотоэлектрический. От выбора метода зависят точность, разрешение и производительность процесса. Аппаратурная точность совмещения может достигать ±0,1 мкм, хотя реально удается получать только ± (0,7 - 0,8) мкм. Для работы авто
Билет 9
Билет 9.1 Особенности магнитных свойств АМС (причина низких значений коэрцитивной силы АМС по сравнению с кристаллическими аналогами)
Магнитомягкость АС
Аморфные ферромагнетики относятся к магнитомягким материалам, т.е. они обладают низкими значениями коэрцитивной силы, высокими значениями магнитной проницаемости. Действительно, рекордные низкие значения коэрцитивной силы были получены именно в железо - никелевых аморфных сплавах достигнуты значения Нс = 0,15 А/м, что является безусловным рекордом, а значения Нс ~ 0.4 -0.5 А/м, (что является рекордом для кристаллических сплавов) встречается довольно часто у АС. Также в АС достигнуты значения проницаемости равные 750 000, что также является рекордным значением.
Причина таких значений кроется в структуре АС. В идеальном аморфном ферромагнетике магнитные моменты расположены как на рис. 1 - параллельно друг другу и направление суммарного магнитного момента в этом случае совпадает с направлением каждого магнитного момента. Такая ситуация никогда не реализуется в кристаллическом состоянии. Во-первых, в кристаллах существует так называемая кристаллографическая анизотропия. Суть ее сводится к тому, что в зависимости от направления внутри кристалла процесс намагничивания этого кристалла происходит с большими или меньшими затратами энергии. Т.е. внутри кристалла есть направления, вдоль которых происходит спонтанная ориентация магнитного момента. Если нет внешних воздействий (внешнего поля, например) то в поликристалле магнитные моменты монокристалликов ориентированы преимущественно вдоль кристаллографических осей легкого намагничивания. В поликристалле эти оси ориентированы случайным образом. Только специальны обработки (например отжиг во внешнем магнитном поле) позволяют уменьшить кристаллографическую анизотропию.
Кроме того, поскольку неупорядоченная аморфная структура макроскопически однородна во всем объеме образца, свойства также должны быть однородными. Однородность структуры проявляется, в частности, в том, что в аморфном состоянии отсутствуют такие дефекты, препятствующие перемещению границ доменов (толщина которых обычно ~102 А), как. границы зерен, поры, включения и т. д. Поэтому при перемагничивании АС движение доменных стенок не осложняется явлением пиннинга стенок на структурных дефектах.
АС можно рассматривать и как материал с очень высокой плотностью дефектов, однако сами дефекты чрезвычайно малы (размером не более нескольких межатомных расстояний) и поэтому доменная стенка оказывается значительно больше , чем размер этих дефектов. В таких условиях стенка как бы не замечает этих дефектов. Если пиннинг и происходит, то он во-первых слабый, а во-вторых он равномерный и усредненный по объему материала. Доменная стенка перемещается в поле постоянной силы, и это не может привести к фиксированию её в каких-то выделенных местах.
Можно ожидать, что именно благодаря этим своим особенностям аморфные ферромагнетики имеют чрезвычайно высокую магнитную проницаемость и низкую коэрцитивную силу.
9.2. Модель Дила-Гроува термического окисления кремния. Получение основного уравнения
Простая и достаточно продуктивная одномерная модель термического окисления кремния была предложена в 1965 г. Дилом и Гроувом. Нам предстоит получить уравнение этой модели, описывающее зависимость толщины слоя двуокиси кремния ХОХ от времени окисления.
Будем различать следующие стадии процесса термического окисления кремния:
· подвод окислителя с потоком газа-носителя к поверхности окисляемой пластины;
· перенос окислителя из газовой фазы в приповерхностный слой растущей плёнки диоксида кремния;
· перенос окислителя через образовавшийся ранее слой окисла к границе SiO2/Si;
· поверхностная химическая реакция окисления кремния на межфазной границе SiO2/Si;
· отвод возможных газообразных продуктов реакции (Н2 ) из зоны реакции в газовую фазу.

Рис.3.1.3. Зависимость толщины слоя диоксида кремния от времени и температуры при окислении кремния в парах воды (а) и в сухом кислороде (б)
Надёжно установлено, что первая и последняя стадии никогда не лимитируют скорость роста слоя диоксида кремния в планарной технологии. При рассмотрении остальных стадий в рамках модели Дила-Гроува полагают:
· концентрация окислителя N (см -3), диффундирующего через растущий слой диоксида кремния, зависит только от расстояния Х до наружной поверхности окисла (одномерное приближение, см. рис. 4);
· процесс окисления протекает в квазистатическом режиме, что позволяет пренебречь потерями потока окислителя на его накопление в растущем слое и считать концентрацию окислителя линейной функцией координаты Х в течение всего процесса.
В соответствии с последним предположением плотность потока окислителя J (см-2с-1) постоянна вдоль всей толщины окисла. Используя обозначения рисунка 3.1.4 , можем записать
 . (3.1.1)
. (3.1.1)
Рассмотрим величину каждого из этих потоков ( индекс проекции вектора плотности потока на ось ОХ будем опускать ).
В первом приближении можно полагать:
 , (3.1.2)
, (3.1.2)
где Н (см/с ) - так называемый коэффициент поглощения окислителя, или коэффициент переноса окислителя из парогазовой фазы в окисел. Разность концентраций ( N * - NО) является стимулом для перехода молекул окислителя через границу раздела ПГС/SiO2. Далее будем полагать, что такой переход не сопровождается диссоциацией молекул окислителя.
Согласно первому закону Фика и предположению о линейности функции N = N(x) имеем:
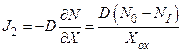 , (3.1.3)
, (3.1.3)
где D (см 2 /с) - коэффициент диффузии окислителя в аморфном диоксиде кремния, ХОХ (см) - текущая толщина окисла.
Поток J3 равен числу молекул окислителя, реагирующих с кремнием в единицу времени на единице поверхности межфазной границы SiO2/Si . В первом приближении полагают
 |
|
|
|
|
|
|
|
|
|
|
|
| |
Рис 3.1.4. Схематическое представление процесса термического окисления кремния согласно модели Дила и Груова.
NO – концентрация окислителя в окисле у границы ПГС/SiO2;
NI - концентрация окислителя в окисле у границы SiO2/Si;
N* - равновесная концентрация окислителя в окисле, соответствующая текущему парциальному давлению окислителя в парогазовой смеси;
J1 – плотность потока окислителя через границу раздела ПГС/SiO2;
J2 – плотность диффузионного потока окислителя через растущей слой окисла;
J3 – плотность потока окислителя, вступающего в химическую реакцию окисления кремния на границе SiO2/Si
 . (3.1.4)
. (3.1.4)
Коэффициент К (см/с) принято называть константой скорости поверхностной химической реакции окисления кремния.
Выразим концентрацию NI через основные параметры процесса окисления. Подставив (3.1.3) и (3.1.4) в условие J2 = J3 , получим
 . (3.1.5)
. (3.1.5)
Подставив (3.1.2) и (3.1.4) в условие J1 = J3 , будем иметь:
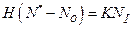 . (3.1.6)
. (3.1.6)
Исключив из (3.1.5) и (3.1.6) концентрацию NO , получим:
 . (3.1.7)
. (3.1.7)
Перейдём теперь к составлению уравнения для скорости роста слоя диоксида кремния. Обозначим через dXOX приращение толщины слоя окисла за время dt, а через no - количество молекул окислителя, необходимое для образования единицы объёма аморфной двуокиси кремния. Оценки показывают, что no ~ 2.5·1022 см -3 , если окислителем является кислород. Если же окислителем является вода, то no будет вдвое больше. Условие материального баланса по окислителю для поверхностной химической реакции, протекающей на границе SiO2/Si можно записать в виде
 . (3.1.8)
. (3.1.8)
Левая часть (3.1.8) выражает количество молекул окислителя, расходуемых за время dt на формирование слоя диоксида кремния толщиной dXOX и площадью 1 см2 . Правая часть (3.1.8) равна количеству молекул окислителя, подведённых путём диффузии через растущий слой окисла к единице поверхности границы SiO2/Si за это же время. Подставляя в (3.1.8) выражение (3.1.4) для потока J3 и используя (3.1.7), получаем дифференциальное уравнение, определяющее зависимость толщины растущего слоя окисла от времени и условий окисления
 . (3.1.9)
. (3.1.9)
Умножим числитель и знаменатель правой части (3.1.9) на 2D/KН и преобразуем его к виду
 , (3.1.10)
, (3.1.10)
где
 , (3.1.11)
, (3.1.11)
 . (3.1.12)
. (3.1.12)
В дальнейшем потребуется выражение для комбинации параметров модели вида В/А
 . (3.1.13)
. (3.1.13)
Величины В и В/А являются основными параметрами модели Дила-Гроува, через которые учитываются условия окисления.
Проинтегрируем уравнение (3.1.10). Будем полагать, что на поверхности пластины в ходе её предварительной обработки был сформирован слой окисла толщиной XOX1 , и эта толщина велика настолько, что предположения рассматриваемой модели становятся допустимыми. Разделим переменные в (3.1.10) и проведём интегрирование в соответственных пределах.
 . (3.1.14)
. (3.1.14)
Из (3.1.14) получаем
 , (3.1.15)
, (3.1.15)
где введено обозначение
 . (3.1.16)
. (3.1.16)
Величина t является ещё одним параметром рассматриваемой модели. Физически содержательное решение квадратного уравнения (3.1.15) имеет вид
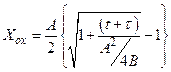 . (3.1.17)
. (3.1.17)
Это основное уравнение модели Дила-Гроува, описывающее зависимость толщины слоя диоксида кремния от времени и условий окисления. Анализ уравнения (3.1.17) позволит установить кинетические закономерности процесса термического окисления кремния, находящие своё объяснение в рамках данной модели.
Билет №9
3.Классификация сигнетоэлектриков.Температурные зависимости диэлектрической проницаемости основных сегнетоэлектриков.Закон Кюри-Вейса.
Дата добавления: 2015-04-18; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |