
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гауссовская случайная величина
P(t)³0.
Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.
2. 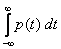 =1.
=1.
Учитывая, что F(+¥)=1, получаем: 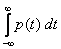 =1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.
=1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.
14. Основные виды распределений дискретных случайных величин (биномиальное распределение, геометрическое распределение, распределение Пуассона) их числовые характеристики.

15. Основные виды распределений непрерывных случайных величин (равномерное, показательное и нормальное распределение) и их числовые характеристики.
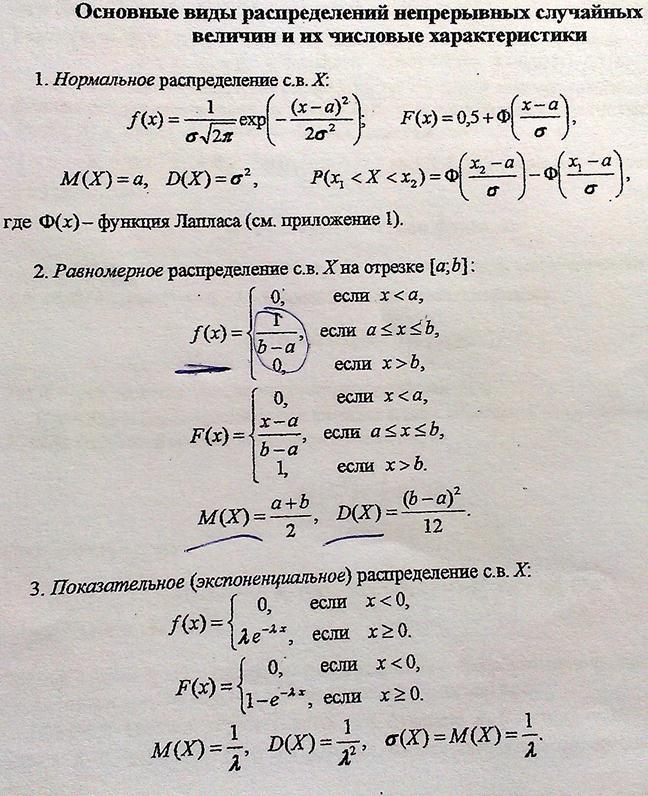
16. Гауссовская случайная величина, ее числовые характеристики. Вероятность попадания гауссовской случайной величины в заданный интервал. Правило «трех сигм».
Гауссовская случайная величина
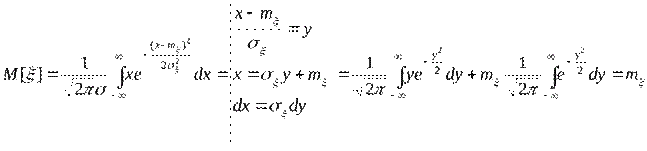
Случайная непрерывная величина X имеет нормальное (гауссово) распределение, если ее плотность распределения вероятности имеет вид
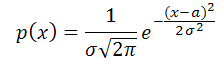
где 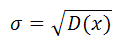 — среднее квадратическое отклонение; а — математическое ожидание.
— среднее квадратическое отклонение; а — математическое ожидание.
Если а=0 и σ=1, то нормальное (гауссовое) распределение называется стандартным нормальным (гауссовым) распределением (таблица плотности вероятности нормальной случайной величины), плотность которого равна
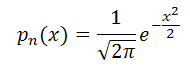
а функция распределения (функция Лапласа) (таблица функции Лапласа)
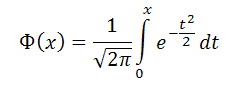
Вероятность попадания в заданный интервал (α;β) нормально распределенной случайной величины с параметрами а, σ вычисляется по формуле:
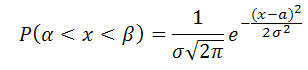
с использованием интеграла вероятности
| P(α<x<β)=F(α)-F(β)=Ф( | β-a | ) |
| σ |
| -Ф( | α-a | ) |
| σ |
Из этих соотношений легко получить вероятность отклонения распределения случайной величины X от своего математического ожидания а:
| P(|X-a|<δ)=2Ф( | δ | ) |
| σ |
,где δ — величина отклонения.
Полагая в этой формуле δ=3σ, получаем
P(|X-a|<δ)=2Ф(3)=2*0.49865=0.9973
Этот результат носит название «правило трех сигм». Таким образом, в 99,7% случаях все значения нормального распределения случайной величины сосредоточены в интервале(-3σ+a; 3σ+a). Распределение, заданное на бесконечном интервале, может быть рассмотрено на конечном интервале, и погрешность при такой замене равно ,примерно, 0,3%.
17. Системы случайных величин. Функция распределения вероятностей системы двух случайных величин (двумерного случайного вектора), ее свойства.
Упорядоченная пара (X,Y) случайных величин X и Y называется двумерной случайной величиной, или случайным вектором двумерного пространства. Двумерная случайная величина (X,Y) называется также системой случайных величина X и Y. Множество всех возможных значений дискретной случайной величины с их вероятностями называется законом распределения этой случайной величины. Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения:
P(X=xi, Y=yj) = pij, i=1,2...,n, j=1,2...,m
Пусть Х = (Х1, Х2,…,ХN) – cовокупность (или система) случайных величин.
Функцией распределения системы случайных величин называется вероятность совместного выполнения неравенств 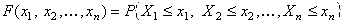 ,
, 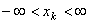 , K = 1, 2, ..., N.
, K = 1, 2, ..., N.
Свойства функции распределения аналогичны свойствам функции распределения одномерной случайной величины. Например, для системы двух случайных величин X и Y:
1) F(х, у) – неубывающая функция своих аргументов;
2) 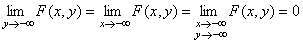 ;
;
3) 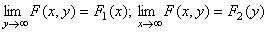 , где F1(X), F2(Y) – функции распределения компонент X и Y;
, где F1(X), F2(Y) – функции распределения компонент X и Y;
4) 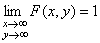 .
.
18. Плотность распределения вероятностей системы двух случайных величин (двумерного случайного вектора), ее свойства.
Предположим, что функция распределения 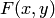 непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции
непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции 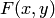
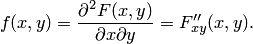
Функция 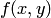 называется плотностью распределения системы непрерывных случайных величин
называется плотностью распределения системы непрерывных случайных величин 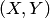 . Зная плотность распределения
. Зная плотность распределения 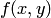 , можно определить вероятность попадания случайной точки
, можно определить вероятность попадания случайной точки 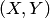 в произвольную область
в произвольную область 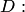
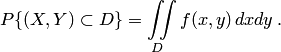
| (5.1) |
Используя формулу (5.1), выразим функцию распределения системы 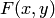 через плотность распределения
через плотность распределения 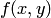 :
:
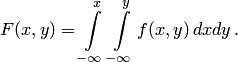
| (5.2) |
Рассмотрим свойства плотности распределения системы двух случайных величин.
Свойство 1. Плотность распределения есть функция неотрицательная: 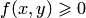 .
.
Свойство 2. Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы равен единице:
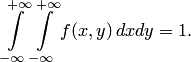
19. Вероятность попадание случайной точки в заданную область (в том числе прямоугольную).
Вероятность попадания случайной точки в заданную область выражаются наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.
Выразим через функцию распределения системы вероятность попадания случайной точки 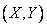 в прямоугольник
в прямоугольник 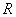 , ограниченный абсциссами
, ограниченный абсциссами 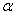 и
и 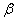 и ординатами
и ординатами 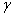 и
и 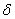 (рис. 8.2.5).
(рис. 8.2.5).
При этом следует условиться, куда мы будем относить границы прямоугольника. Аналогично тому, как мы делали для одной случайной величины, условимся включать в прямоугольник 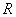 его нижнюю и левую границы и не включать верхнюю и правую. Тогда событие
его нижнюю и левую границы и не включать верхнюю и правую. Тогда событие 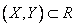 будет равносильно произведению двух событий:
будет равносильно произведению двух событий: 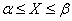 и
и  . Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости
. Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости 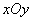 четыре бесконечных квадранта с вершинами в точках
четыре бесконечных квадранта с вершинами в точках 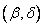 ;
; 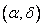 ;
; 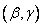 и
и 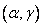 (рис. 8.2.6).
(рис. 8.2.6).
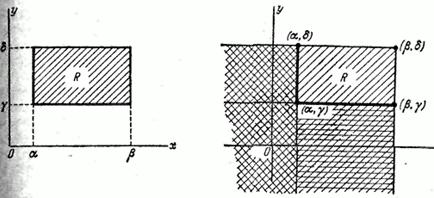
Рис. 8.2.5. Рис. 8.2.6
Очевидно, вероятность попадания в прямоугольник 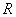 равна вероятности попадания в квадрант
равна вероятности попадания в квадрант 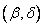 минус вероятность попадания в квадрант
минус вероятность попадания в квадрант 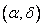 минус вероятность попадания в квадрант
минус вероятность попадания в квадрант 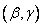 плюс вероятность попадания в квадрант
плюс вероятность попадания в квадрант 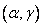 (так как мы дважды вычли вероятность попадании в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:
(так как мы дважды вычли вероятность попадании в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:
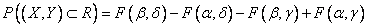 .
.
20. Независимость нескольких случайных величин. Связь с коэффициентом корреляции.
Случайные величины 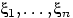 называют независимыми (в совокупности), если для любого набораборелевских множеств
называют независимыми (в совокупности), если для любого набораборелевских множеств 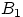 , ...,
, ..., 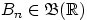 имеет место равенство:
имеет место равенство:
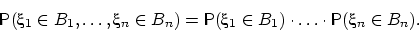
Коэффициент корреляции - это сила и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между - 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной, а когда значение r отрицательно, связь также отрицательна. Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует.
21. Ковариация, коэффициент корреляции, их свойства. Условные законы распределения.
Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин
Так как и — независимые случайные величины, то и их отклонения и также независимы. Пользуясь тем, что математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей, а математическое ожидание отклонения равно нулю, имеем
Свойства ковариации:
Ковариация двух независимых случайных величин и равна нулю[
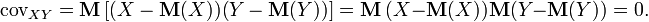
Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий: 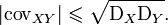

Дата добавления: 2015-04-18; просмотров: 642; Мы поможем в написании вашей работы!; Нарушение авторских прав |