Пример 3. Доверительный интервал для математического ожидания.

Пусть задана выборка некоторой случайной величины , арактеристики которой (дисперсия D и математическое ожидание M) неизвестны. Эти параметры оценим так:

- несмещенная оценка дисперсии.

Величину называют оценкой среднего квадратического отклонения. Воспользуемся тем, что величина представляет собой сумму независимых случайных величин, и, согласно центральной предельной теореме, при достаточно большом ее закон близок к нормальному. Поэтому будем считать, что величина распределена по нормальному закону. Характеристики этого закона - математическое ожидание и дисперсия - равны соответственно M (настоящее МО случайной величины ) и .

Найдем такую величину , для которой . Перепишем это в эквивалентном виде и скажем, что случайная величина перед знаком неравенства есть модуль от стандартной нормальной. Получаем, что , и . В случае неизвестной дисперсии ее можно заменить на оценку .

Квантили стандартного нормального распределения:

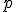
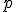
	Квантиль порядка		Квантиль порядка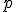
0.01	-2.326348	0.60	0.253347
0.025	-1.959964	0.70	0.524401
0.05	-1.644854	0.80	0.841621
0.10	-1.281552	0.90	1.281552
0.30	-0.524401	0.95	1.644854
0.40	-0.253347	0.975	1.959964
0.50		0.99	2.326348

Например, выбирая , получаем коэффициент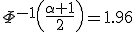

Окончательно: с вероятностью можно сказать, что

31. Доверительное оценивание параметров нормального распределения.

32. Оценка вероятности появления события по частоте в n независимых опытах.

При проведении экспериментов часто приходится оценивать неизвестную вероятность события P по его частоте в N независимых экспериментах. Частота некоторого события в N независимых экспериментах есть не что иное, как среднее арифметическое наблюдаемых значений величины Х, которая в каждом отдельном опыте принимает значение 1 (если событие совершилось), или значение 0 (если событие не произошло):

В [1] показано, что математическое ожидание величины Х равно Р, а ее дисперсия равна Р(1-P). Математическое ожидание выборочного среднего равно Р:

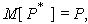
т.е. оценка является несмещенной. Дисперсия величины равна:

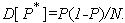
Специфика этой задачи в том, что Х в данном случае - дискретная случайная величина только с двумя возможными значениями: 0 и 1. Сделаем ограничение практически всегда выполняемым - число экспериментов достаточно велико, так что выполняются условия:

N(1-P) > 4, NP > 4.

Если эти условия выполнены, то частоту можно считать распределенной по гауссовскому закону. Тогда параметры этого закона:

В [1] приведена методика оценки доверительного интервала, которую мы приведем далее. Границы интервала, в котором заключено истинное значение вероятности события, определяются следующим образом:

,
.

Здесь - конкретная оценка вероятности (частоты события), а t находится, исходя из заданной доверительной вероятности :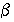

.

33. Основы теории проверки статистических гипотез. Понятие статистического критерия, критической области.

34. Критерий согласия Хи-квадрат о виде распределения.

Критерий согласия Пирсона χ² – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (f_Т) и эмпирическими (f) частотами к теоретическим частотам:

· k–число групп, на которые разбито эмпирическое распределение,

· f_i–наблюдаемая частота признака в i-й группе,

· f_T–теоретическая частота.

35. Критерий согласия Романовского.

Критерий Романовского с основан на использовании критерия Пирсона, т.е. уже найденных значений , и числа степеней свободы df:

Он удобен при отсутствии таблиц для .
Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.