Условные законы распределения

Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:

Перейдем теперь к решению обратной задачи: по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними.

Таким образом, если случайные величины 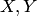взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения.

Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается , условная плотность распределения — 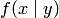(мы записали условные законы распределения случайной величины 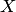при условии, что другая случайная величина приняла определенное значение).

Плотностью распределения для случайной величины 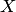при условии, что случайная величина приняла определенное значение (условной плотностью распределения), назовем величину

Аналогично плотностью распределения для случайной величины при условии, что случайная величина 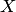приняла определенное значение, назовем величину

. Отсюда получаем .

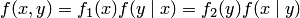или с учетом формул (5.3)

Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,

22. Числовые характеристики случайных величин и их свойства.

23. Неравенство Чебышева. Закон больших чисел в форме Чебышева.

Одно из основных утверждений закона больших чисел состоит в том, что значение среднеарифметического случайных величин с равными математическими ожиданиями 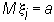при большом n (при некоторых широких условиях) оказывается приближенно равным a:

уточним: будем писать

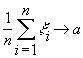при ,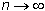

если для любого e >0 и достаточно больших n соотношение

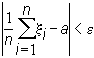(2)

выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:

при .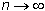

это одно из утверждений закона больших чисел. Заметим, что, как и теорема Бернулли, оно не означает, что соотношение (2) достоверно; однако, если n достаточно велико, то вероятность его выполнения близка к 1, например, 0.98 или 0.999, что означает практически достоверно.Приведем полную формулировку одной из теорем закона больших чисел в форме Чебышева,

24. Характеристическая функция, ее свойства.

Свойства характеристических функций[править | править исходный текст]

• Характеристическая функция однозначно определяет распределение. Пусть 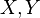суть две случайные величины, и . Тогда . В частности, если обе величины абсолютно непрерывны, то совпадение характеристических функций влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение характеристических функций влечёт совпадение функций вероятности.
• Характеристическая функция всегда ограничена:

.

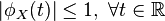• Характеристическая функция в нуле равна единице:

.

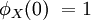• Характеристическая функция всегда непрерывна: .
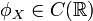• Характеристическая функция как функция случайной величины однородна:

.

• Характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций. Пусть суть независимые случайные величины. Обозначим 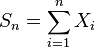. Тогда

.

• Для всех вещественных верно равенство , где означает комплексно сопряжённую с функцию^[1].
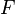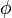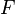• Теорема обращения (Леви). Пусть - функция распределения, а - её характеристическая функция. Если и - точки непрерывности , то

25. Основные задачи математической статистики. Эмпирическая функция распределения. Гистограмма, полигон частот. Выборочные характеристики.

26. Задачи теории оценивания. Точечное оценивание. Свойства точечных оценок.

Оценкапараметра — соответствующая числовая характеристика, рассчитанная по выборке. Когда оценка определяется одним числом, она называется точечной оценкой.

Свойства точечных оценок[

Оценка 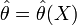называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:

,

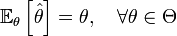где 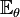обозначает математическое ожидание в предположении, что 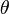— истинное значение параметра (распределения выборки ).

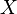• Оценка 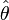называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.
• Оценка 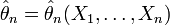называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: ,

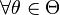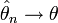по вероятности при .

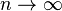• Оценка 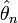называется сильно состоятельной, если ,

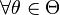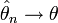почти наверное при .

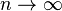Надо отметить, что проверить на опыте сходимость «почти наверное» не представляется возможным, поэтому с точки зрения прикладной статистики имеет смысл говорить только о сходимости по вероятности.

27. Оценки математического ожидания и дисперсии, их свойства.

Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет математическое ожидание Mx = m, является несмещенной оценкой этого параметра.

Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет Mx = m и , является состоятельной оценкой этого параметра.

Если случайная выборка состоит из n независимых наблюдений над случайной величиной x с

Mx = m и Dx = , то выборочная дисперсия

(23.3)

не является несмещенной оценкой Dx - генеральной дисперсии.

28. Метод моментов.

29. Метод максимального правдоподобия.

30. Интервальное (доверительное) оценивание.