Расчет режимов сложнозамкнутых электрических сетей

Общие сведения.

Сложнозамкнутая сеть – сеть, имеющая узловые точки. Узловая точка – точка, которая имеет не менее трех ответвлений, не считая нагрузку. Участок сети, между узловыми точками, или между узл. точ. и и питающим пунктом – ветвь. Расчет рабочего режима такого класса сетей сводится к определению потокораспределения и нахождению U в узловых точках сети и проводится в несколько этапов:

1 – определяется предварительное распределение мощностей (I) по участкам сети и по нему находят точки потокораздела (0 итерация). Этот расчет проводят без учета потерь мощности в сети и падения U. Основные методы расчета:

- метод контурных S (I);

- метод узловых напряжений;

- метод преобразования сети.

2 – затем, начиная с (∙) потокораздела уточняют распределение S с учетом потерь, двигаясь от (∙) раздела к питающему пункту (пунктам). Расчет без учета падения U-я.

3 – начиная с пункта питания, определяют распределение U-я вдоль сети с учетом из потерь и уточняют распределение S, двигаясь от пункта питания к (∙) потокораздела. Если относительная погрешность не превышает заданную, то расчет останавливают, в другом случае проводят следующую итерацию.

Метод контурных мощностей.

При 0-й итерации пренебрегают потерями мощности и U на участках сети. С учетом этих допущений расчет ведут по следующему алгоритму:

1. Задаются условными «+» направлением линейных S(I) на каждом из участков сети и обозначают их на расчетной схеме.

2. Определяют число независимых контуров, которые = числу ветвей в сети – число узловых точек.

3. Выбирают эти контуры и задаются их направлениями обхода.

4. Полагая, что в каждом контуре протекает своя контурная S(I) задаютсяих направлением обхода.

5. Составляют на основании II ЗК для каждого независимого контура расчетные уравнения относительно линейных мощностей.

6. Выражают линейные S(I) ч/з контурные S(I) и мощности нагрузок.

7. Подставляют в уравнение из п. 5 вместо линейных S(I) их значения из п.6 → система, в которой неизвестны контурные S(I) → решая ее, определяют S(I).

8. Используя выражение, полученное в п. 6, определяют линейные S(I) и по ним находят точки потокораздела.

9. Делают проверку на основании уравнений, составленных по II ЗК для каждого независимого контура относительно линейных S(I) (п.5).

Метод узловых потенциалов

За неизвестные принимаем U в узл. (∙) сети. Расчет проводится с учетом допущений: пренебрегают потерями S в сети и U-я. Алгоритм:

1. Задаются узловыми U-ми во всех узл. (∙) и обозначают их на схеме.

2. Задаются направлением лин. S(I) и обозначают их на расчетной схеме.

3. Для каждой узл. (∙) составляют ур-е по I ЗК в отношении линейных S(I) и нагрузочных S(I).

4. Считая каждую ветвь в сложнозамкнутой сети, как сеть с двусторонним питанием, определяют линейные S(I), используя формулы, позволяющие находить S(I), вытекающие из питающих пунктов.

5. Подставляя выражение, полученное в п. 4, в уравнения из п. 4, получим расчетные ур-я, в которых в качестве неизвестных будут узловые U-я. Число уравнений всегда = числу неизвестных узловых уравнений.

6. Решая уравнения, находим узловые U-я.

7. Используя ур-я, полученные в п. 4, определяют линейные S(I) ч/з узл. U-я, заданные сопротивления и нагрузочные мощности.

8. Проверка на основании уравнений, составленные по I ЗК для узловых точек сети.

Особенности рачета методами контурных S(I) и узловых U.

1. Алгоритмы справедливы, если сети имеют 1 источник питания. В этом случае необходимо составить дополнительные уравнения: для каждого питающего пункта с заданным U (кроме базисного узла – один из узлов, где задано напряжение [балансирующий узел ??? ] ) составляются уравнения, выражающие напряжение в этом узле ч/з уравнение балансирующего узла ­«–» суммарное падение U-е м/у балансирующим и рассматриваемым узлом.

Метод преобразования сети

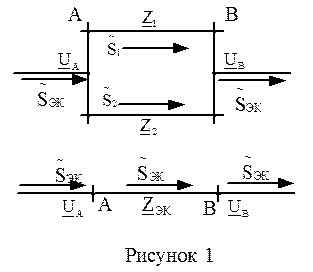Данный метод является наиболее универсальным, т.к. его можно использовать не только для определения потокораспределения и при расчете 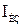, анализа устойчивости электрических систем и ряда других задач. Суть метода заключается в сведении сложнозамкнутой сети, путем последовательных эквивалентных преобразований в сети с двусторонним питанием с последующим определением потокораспределения. После этого, посредством обратных последовательных преобразований по найденному потокораспределению в сети с двусторонним питанием, находят действительное потокораспределение. Теоретическое положения метода преобразования основаны на:

1. На замене || участков сети при отсутствии на них || нагрузок одним участком (рис.1);

;

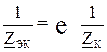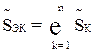
Обратное преобразование:

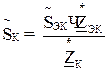
2. На замене последовательных участков сети (при отсутствии присоединенных нагрузок):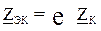

3. На замене участков сети, соединенных по схеме Δ в эквивалентную Υ в случае, если не присоединенных нагрузок.

При Δ→Υ:

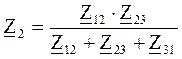
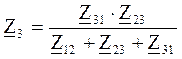
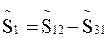
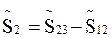
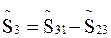
При Υ→Δ

; ; ; ; ; .

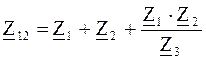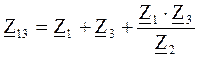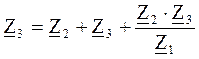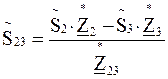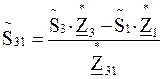4. На замене источников U-я, присоединенным к одной точке сети одним эквивалентным источником:

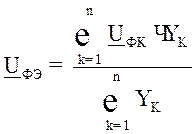, где 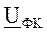- напряжение источников, подключенных к рассматриваемому узлу, 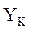- проводимость ветви, подходящей к данному узлу. Обратная задача заключается в том, что по эквивалентному значению тока, найти токи, протекающие по участкам: 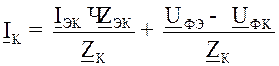. Если U-е питающих пунктов одинаково, то их можно объединить в один, аналогично, один питающий пункт можно разделить на любое число питающих пунктов.