
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диапазоны значений целых чисел со знаком
| Формат числа в байтах | Диапазон | |
| Запись с порядком | Обычная запись | |
| –27 ... 27–1 | –128 ... 127 | |
| –215 ... 215–1 | –32768 ... 32767 | |
| –231 ... 231–1 | –2147483648 ... 2147483647 |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:
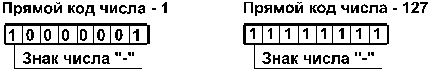
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:
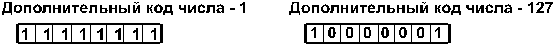
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Для вещественных данных обычно используются две формы записи: число с фиксированной точкой (ЧФТ) и число с плавающей точкой (ЧПТ).
Числа с фиксированной точкой.
Форма записи числа с фиксированной точкой использовалась в основном на ранних этапах развития вычислительной техники. Запись числа с фиксированной точкой обычно имеет знаковый и цифровой разряды. Фиксированная точка означает, что на этапе конструирования ЭВМ было определено, сколько и какие разряды машинного слова отведены под изображение целой и дробной частей числа. Запятая в разрядной сетке может быть зафиксирована, в принципе, после любого разряда.
Как частный случай числа с фиксированной точкой может быть рассмотрена запись целого числа (в этом случае все разряды, кроме знакового, используются для записи целой части).
К достоинствам использования чисел с фиксированной точкой относятся простота выполнения арифметических операций и высокая точность изображения чисел. К недостаткам - небольшой диапазон представления чисел.
Числа с плавающей точкой.
Для представления чисел с плавающей точкой (ЧПТ) используется полулогарифмическая форма записи числа:
N = ± mq ± p
где q- основание системы счисления, p - порядок числа, m - мантисса числа N.
Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или вправо.
Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: 1/q ≤ | m | < 1. Таким образом, в нормализованных числах цифра после точки должна быть значащей.
Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка:
а) представление чисел в формате полуслова
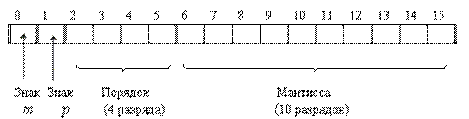
б) представление чисел в формате слова
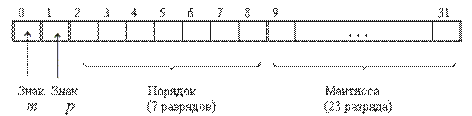
Наиболее типично представление ЧПТ в формате слова (32 разряда).
Пример.
Число А=-3.510=-11.12=-0.111·1010
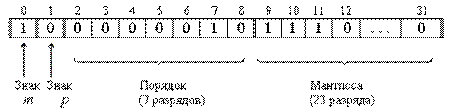
Максимальным числом представимым в формате слова будет A=(0.1111...1·101111111)2(1·2127)10.
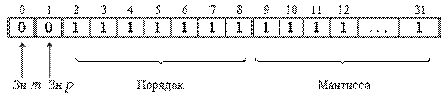
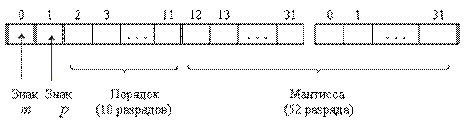
Таким образом, числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от -1·2127 до 1·2127 (21271038), а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
Дата добавления: 2015-04-18; просмотров: 309; Мы поможем в написании вашей работы!; Нарушение авторских прав |