Функция Эйлера. Теорема Эйлера. Малая теорема Ферма. Понятие простого числа и взаимопростых чисел. Алгоритмы Эвклида поиска НОД двух и большего числа целых чисел.

Функция Эйлера , где — натуральное число, равна количеству натуральных чисел, меньших и взаимно простых с ним. Названа в честь Эйлера, который впервые использовал ее в своих работах по теории чисел.

Числовая функция j(m), для каждого целого числа m, m>1 ,представляющая собой количество чисел из совокупности чисел 0,1,…,m -1 взаимно простых с m называется функцией Эйлера. Например: j(2)=1, j(3)=2, j(4)=2, j(5)=4, j(6)=2 и т.д.

Очевидно, что если m=p - простое число, тоj(p)=p-1. Название функции j(m) происходит из следующей теоремы Эйлера: Для любых целых чисел а и m, таких, что (a,m)=1 (т.е. a и m взаимно простые числа) справедливо выражение

Из теоремы Эйлера следует малая теорема Ферма: Если р - простое число и , то . Это утверждение очевидно, если вспомнить, что для простого числа р, 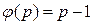.Наименьшие из чисел 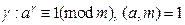называется показателем числа а по модулю m. Существование таких чисел 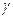обеспечивается указанной выше теоремой Эйлера. Если показатель числа а по модулю m равен 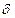, то тогда и только тогда, когда . Показатель числа а по модулю m является делителем числа . Если показатель числа a по модулю m равен 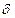, то показатель числа a^k равен 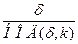для произвольного целого k. В частном случае, когда показатель числа а по модулю m равен j(m), то а называется первообразным (примитивным) корнем по модулю m. Если р – простое число, и число а является первообразным корнем по модулю Р, то любой элемент b из множества чисел 1,2,…,р -1 имеет однозначное представление в виде для некоторого целого числа х 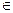{0,1,…,р -1}.

Число х при этом называется дискретным логарифмом (или индексом) числа b по основанию а.

Сложность вычисления дискретных логарифмов совпадает со сложностью нахождения разложения целого числа на простые сомножители и имеют exp сложность, что определяет широкое применение таких задач при построении современных криптосистем

Число m называется псевдослучайным по основанию а, если и (р – простое число). Существуют составные числа m, являющиеся псевдослучайными для всех а, взаимно простых с m. Такие числа называются числами Кармайкла. Например, 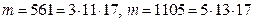. Если t различных оснований а₁,…,а_t выбираются независимо и случайно, то составное число m выдержит тест Ферма i=1,…,t с вероятностью

Многочленом называется выражение вида

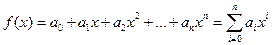
- коэффициенты;

х – переменная;

n - степень многочлена, обозначаемая degf(x)

Теорема. 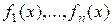- многочлены, не все равные нулю. Тогда существует однозначно определенный нормативный многочлен d(x), обладающий свойствами

1.d(x) делит каждый многочлен .

2.Любой многочлен g(x), который делит каждый из многочленов , делит и многочлен d(x).

Нормированный многочлен d(x) называют наибольшим общим делителем многочленов 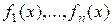и обозначают НОД( 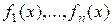). Если НОД( 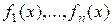)=1, то многочлены 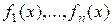называются взаимно простыми. Они называются попарно взаимно простыми, если

.

Наибольший общий делитель двух многочленов (также как и двух целых чисел) можно найти при помощи алгоритма Евклида. Пусть многочлен g(x)¹0 и не делит многочлен f(x).

Тогда, применяя многократно алгоритм деления многочленов с остатком, получим

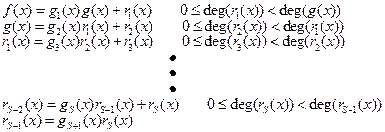
Т.к. степень deg(g(x)) конечна, то процедура заканчивается за конечное число шагов. Если старший коэффициент последнего ненулевого остатка равен b, то .

Если у нас более чем 2 многочлена (n>2), то НОД( 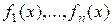) при ненулевых многочленах 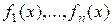находят (как и для целых чисел), применяя расширенный алгоритм Евклида: сначала определяют НОД( ), а затем находят последовательно, применяя алгоритм Евклида,

НОД(НОД( ))=НОД( ) и т.д.

Пример: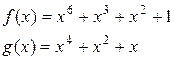

Найдем НОД( ) по алгоритму Евклида

Значит, НОД( )=1 т.е. многочлены f(x) и g(x) взаимно простые.

(1)

.

Ма́лая теоре́ма Ферма́ — классическая теорема теории чисел, которая утверждает, что

Если p — простое число, и 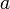не делится на 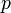, то Другими словами, при делении нацело на 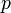даёт в остатке 1.

Равносильная формулировка:

Для любого простого 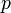и целого : делится на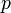

Из теоремы Эйлера следует малая теорема Ферма: Если р- простое число и p / a, то a p−1 ≡1(mod p). Это утверждение

очевидно, если вспомнить, что для простого числа р,

ϕ ( p) = p −1.Наименьшие из чисел γ : aγ ≡1(modm), (a,m) =1

называется показателем числа а по модулю m. Существование таких чисел γ обеспечивается указанной выше теоремой Эйлера. Если показатель числа а по модулю m равен δ , то aγ ≡ aβ (modm) тогда и только тогда, когда γ = β (modδ ) . Показатель числа а по модулю m является делителем числа ϕ (m) . Если показатель числа a по модулю m равенδ , то показатель числа ak равен

для произвольного целого k. В частном случае, когда показатель числа а по модулю m равен ϕ(m), то а называется первообразным (примитивным) корнем по модулю m.

Если р – простое число, и число а является первообразным корнем по модулю Р, то любой элемент b из множества чисел 1,2,…,р -1 имеет однозначное представление в виде b ≡ ax (mod P) для некоторого целого числа х∈{0,1,…,р -1}.

Число х при этом называется дискретным логарифмом (или индексом) числа b по основанию а.