Простейшие помехоустойчивые коды

Введение в коды избыточности можно осуществлять по различным правилам. Одним и наиболее часто используемым правилом является правило проверки на четность числа единиц в кодовой комбинации (разрешенной). Комбинации этого кода образуются путем добавления к m информационным эле-

ментам (битам в случае двоичного кода) одного проверочного (m+1) бита, так чтобы полное число единиц в кодовой комбинации было четным. Схемная реализация кодеров и декодеров линейного блочного кода Хэмминга показана на рисунке 1.22

Основной задачей при построении линейных блочных кодов как и любых других помехоустойчивых кодов является разработка правил формирования проверочных элементов. Напомним, что эти правила заключаются в том, чтобы в результате проверок на четность числа единиц в передаваемой кодовой комбинации можно было указать позиции (номера) искаженных элементов.

Последовательность кодовых комбинаций первичного m разрядного кода сообщения можно записать в виде матрицы

Чтобы не записывать все кодовые комбинации этой матрицы можно за-

писать единичную матрицу размером m×m.

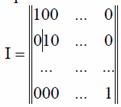
а все кодовые комбинации матрицы А получить путем поэлементного сложения по модулю 2 строк единичной матрицы I во всех возможных сочетаниях. Общее число таких сложений

Циклические коды – это разновидность линейных блочных кодов ипредназначены они для обнаружения и исправления ошибок.

К числу эффективных кодов, обнаруживающих одиночные, кратные ошибки и пачки ошибок, относятся циклические коды (CRC - Cyclic Redundance Code). Они высоконадежны и могут применяться при блочной синхронизации, при которой выделение, например, бита нечетности было бы затруднительно.

Один из вариантов циклического кодирования заключается в умножении исходного кода на образующий полином g(x), а декодирование - в делении на g(x). Если остаток от деления не равен нулю, то произошла ошибка. Сигнал об ошибке поступает на передатчик, что вызывает повторную передачу.

Образующий полином есть двоичное представление одного из простых множителей, на которые раскладывается число Xⁿ-1, где Xⁿ обозначает единицу в n-м разряде, n равно числу разрядов кодовой группы. Так, если n = 10 и Х = 2, то Xⁿ-1 = 1023 = 11*93, и если g(X)=11 или в двоичном коде 1011, то примеры циклических кодов A_i*g(Х) чисел A_i в кодовой группе при этом образующем полиноме можно видеть в следующей табл. 3.1.

Основной вариант циклического кода, широко применяемый на практике, отличается от предыдущего тем, что операция деления на образующий полином заменяется следующим алгоритмом: 1) к исходному кодируемому числу А справа приписывается К нулей, где К - число битов в образующем полиноме, уменьшенное на единицу; 2) над полученным числом А*(2^К) выполняется операция О, отличающаяся от деления тем, что на каждом шаге операции вместо вычитания выполняется поразрядная операция "исключающее ИЛИ": 3) полученный остаток В и есть CRC - избыточный К-разрядный код, который заменяет в закодированном числе С приписанные справа К нулей, т.е.

С= А*(2^К)+В