Свойства.

Во-первых, сигмоидальная функция изменяется в диапазоне (0,1) и, тем самым, позволяет сжимать произвольный диапазон изменения аргумента y(t)или V(t)в диапазон (0,1) для выходного сигнала z(t), что весьма удобно при моделировании и аппаратно-программной реализации нейронных сетей на ЭВМ (отсюда название - «сжимающая»функция).

Во-вторых, сигмоидальная функция непрерывна и дифференцируема во всем диапазоне изменения аргумента и имеет очень простое выражение для производной:

Это свойство позволяет использовать ее в широко распространенных градиентных алгоритмах обучения искусственных нейронных сетей, требующих операций многократного дифференцирования.

В третьих, сигмоидальная функция обладает свойством автоматического регулирования усиления для входных сигналов разного уровня. Центральный участок функции, соответствующий области малых входных сигналов, имеет большой наклон кривой и максимум производной, поэтому коэффициент усиления здесь максимален. По мере удаления от центрального участка функции в область больших по модулю входных сигналов, наклон кривой и ее производная уменьшаются, соответственно уменьшается и коэффициент усиления. Иными словами, один и тот же нейрон или одна и та же сеть нейронов могут эффективно отрабатывать как сильные, так и слабые сигналы.

Графики сигмоидальной функции при а=1 приведены на рис. 3.8.

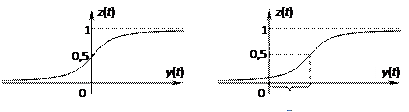Рис. 3.8. Графики сигмоидальной функции при а=1

График производной сигмоидальной функции имеет колоколообразную форму (рис. 3.9).

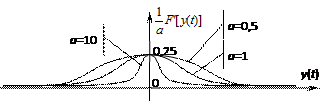Рис. 3.9. График первой производной сигмоидальной функции

4. Функция гиперболического тангенса (S-образная, сигмоид).

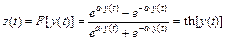
или

.

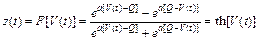Графики функции гиперболического тангенса при a=1 показаны на рис. 3.10. По форме и свойствам эта функция сходна с предыдущей. Отличие заключается в том, что она симметрична относительно нуля, принимает значения различных знаков и имеет двойной размах по амплитуде, что эффективно используется для ряда нейронных сетей. Коэффициент а, как и для предыдущей функции, характеризует степень крутизны функции.

Производная функции гиперболического тангенса равна

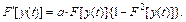
Рис. 3.10. Графики функции гиперболического тангенса

График производной этой функции имеет такой же вид, как и для сигмоидальной функции (см. рис.